¿DICE LA BIBLIA QUE Pi = 3?
2 participantes
Página 1 de 1.
 ¿DICE LA BIBLIA QUE Pi = 3?
¿DICE LA BIBLIA QUE Pi = 3?
“El rostro de Pi estaba enmascarado; se sobreentendía que nadie podía contemplarlo y continuar con vida. Pero unos ojos de penetrante mirada acechaban tras la máscara, inexorables, fríos y enigmáticos.” Bertrand Russell
“La Geometría existía antes de la Creación. Es co-eterna con la mente de Dios… La Geometría ofreció a Dios un modelo para la Creación… La Geometría es Dios mismo.” Johannes Kepler
Visualización de la definición de π. Es el perímetro de una circunferencia de diámetro 1.
Pasajes bíblicos: A menos que se indique lo contrario, pertenecen a la traducción Reina Valera 1960
Ver I Reyes cap. 7
Ver 2 Crónicas cap. 4
Introducción
La pregunta si la biblia dice que Pi=3, no es difícil de responder. Al principo me pareció que no lo iba a entender, pero a medida que fui investigando, fui hallando mas información de la que yo me imaginaba,
El interés de este artículo es el fuerte ataque de los ateos que pretenden con esto probar que la Biblia está equivocada y derribar la doctrina de la inspiración divina y la inerrancia de las escrituras. Dos doctrinas sumamente importantes a la hora de realizar exégesis bíblica o de una correcta apologética del cristianismo.
Vemos que podemos deducir del estudio de este pasaje bíblico para hallar una óptima respuesta. Este pasaje (I Reyes cap. 7:23), está en el contexto de la narración de la construcción del templo de Salomón. Un hermoso templo que este rey construyó, en un periodo de 13 años. Ya su padre, el rey David había querido hacerlo, pero el Señor no se lo permitió, pues había derramado demasiada sangre de sus enemigos. Por lo tanto, solo pudo comprar el terreno, y destinar los recursos para que su hijo Salomón inicie la construcción.

Representación del Templo de Jerusalén reconstruido por Herodes
Pablo Hoff comenta que «El templo de Salomón se asemejaba algo a los templos paganos, pero con algunas diferencias importantes. En el templo salomónico, no se encontraba asomo alguno de idolatría. En el lugar santísimo no había imagen ni representación alguna de Dios, pues Dios es espíritu y no se le puede representar materialmente. »[0]
El diccionario bíblico explica que «en la Mesopotamia, de donde salió Abraham, cada ciudad tenía un templo dedicado a su deidad patronal. Se consideraba que ese dios era el propietario de la tierra, y si no recibía su bendición esa tierra habría de resultar improductiva, lo cual daría como resultado ingresos pobres para su templo. El rey o gobernante local actuaba como mayordomo del dios. No tenía sentido que los patriarcas seminómades edificasen un santuario fijo para su Dios. Él se les revelaba en los lugares y en la forma que a él le placía. A veces esas ocasiones ofrecían motivo para la erección de un altar para sacrificios. A veces se conmemoraba dicho acontecimiento con una columna (Gn. 28.22, VRV2 “piedra”).
Una vez que Israel adquirió características de nación se hizo necesario contar con un santuario central, un lugar de reunión para todo el pueblo, símbolo de su unidad en el culto a su Dios. Esta necesidad la suplió primero el tabernáculo durante la peregrinación por el desierto, y luego los santuarios reconocidos durante el periodo de los jueces (p. cj. Siquem, Jos. 8.30ss; 24.1ss; Silo, 1 S. 1.3).
Las naciones de Canaán tenían sus propios templos, llamados simplemente “casa de Dagón” o casa de la deidad que fuera patrona de la ciudad correspondiente (hcb. bét Aagon, 1 S. 5.5; bét ‘astarót, 1 S. 31.10; cf. bét yhwh, Ex. 23.19). Se han encontrado varios de estos templos en Bet-sán, Hazor, y otros sitios.
Tintoretto: «La reina de Saba y Salomón» (ca. 1555). Museo del Prado
La falta de un santuario dedicado a Yahvéh aparecía como una afrenta cuando David hubo consolidado su posición y edificó un palacio permanente para sí mismo. Dijo entonces el rey *yo habito en casa de cedro, y el arca de Dios está entre cortinas” (2 S. 7.2). No le fue dado el que edificase el templo, porque sus propias manos estaban teñidas de la sangre de sus enemigos, pero él reunió los materiales, reunió fondos, y adquirió un lugar adecuado (1 Cr. 22.8, 3; 2 S. 24.18-25). Salomón inició la construcción en el año cuarto, y el templo se completó siete años después (I Re. 6.37-38).
El templo de Salomón, el que se encontraba en la zona llamada ahora “Haram esh-Sherif” en el lado oriental de la “ciudad antigua” de Jerusalén es algo que no se discute. La ubicación precisa dentro del vasto recinto resulta más incierta. La parte más alta de la roca (ahora cubierta por el edificio conocido como “La cúpula de la roca”) puede haber sido el lugar del santuario de mas adentro o del altar de los holocaustos. en la parte exterior (2 Cr. 3:1). Presumiblemente esta roca constituía parte de la era de Arauna,comprada por David por uina suma que se indicaba en cincuenta ciclos de Plata ( 2 Sam. 24:24) o 600 ciclos de oro (I Cro. 21:25)
De la estructura de Salomón no queda nada en pie, y durante las excavaciones auspiciadas por el Fondo para la Exploración de la Palestina no se encontraron rastros concretos de la misma. Más aun, es probable que la tarea de nivelar la roca y de edificar los grandes muros de apoyo para el atrio del templo de Herodes hayan borrado todo vestigio de construcciones anteriores.
Los pasajes de 1 R. 6-7 y 2 Cr. 3-4 deben servir de base para cualquier reconstrucción del templo de Salomón. Dichos relatos, si bien detallados, no abarcan todos los aspectos, no se entienden perfectamente, y contienen algunas aparentes discrepancias (p. ej. 1 R. 6.2 y I6s). Pueden ser complementadas con referencias incidentales, y por la descripción del templo de Ezequiel, versión ampliada del edificio de Salomón (Ez. 40-43). El templo propiamente dicho era rectangular, orientado de E a O. Es razonable suponer que, como el templo de Ezequiel, se encontraba sobre una plataforma (cf. Ez. 41.Ocho). No se dan las dimensiones de la zona circundante. Siguiendo nuevamente el plano de Ezequiel, parecería que hubo dos patios, interior y exterior; sugerencia apoyada por 1 R. 6.36; 7.12; 2 R. 23.12; 2 Cr. 4.9.
Maqueta del Templo
EL REY SALOMÓN Y SU TEMPLO
El altar de bronce para los sacrificios se encontraba en el patio interior (1 R. 8.22,64; 9.25). Tenía 20 codos de lado, y 10 codos de altura (2 Cr. 4.1). Entre este y el pórtico se encontraba la fuente de bronce que contenía el agua para las purificaciones rituales (el “mar … fundido”, 1 R. 7.23-26). Este gran receptáculo, de 10 codos de diámetro, descansaba sobre cuatro grupos de cuatro bueyes de bronce orientados hacia los cuatro puntos cardinales. Fueron retirados por Acaz (2 R. 16.17).
En la dedicación del templo Salomón se ubicó sobre un “estrado” (2 Cr. 6.12s, heb. kiyyor, palabra que se usa para “fuente” en otras partes, Ex. 30.18, etc.; aquí puede significar fuente invertida), lo cual tiene paralelos en las esculturas sirias y egipcias, y posiblemente en las acádicas (véase W. F. Albnght, Archaeology and the Religión of lsraeL, 1953, pp. 152-154).
Una serie de escalones probablemente llevaba del patio interior al pórtico (heb. ‘úlam). La entrada tenía dos columnas, Jaquín y Boaz, con capiteles profusamente ornamentados. Su función es incierta; no constituían parte de la estructura. Es probable que hubiera puertas para cerrar el pasillo (cf. Ez. 40.48).
El pórtico medía 10 codos de largo y 20 codos de ancho (sobre la longitud del codo, véase pesos y medidas). Su altura se indica como 120 codos (2 Cr. 3.4), pero seguramente se trata de un error, porque el resto del edificio sólo tenía 30 codos de altura. Al O del pórtico se encontraba la gran cámara en la que se llevaban a cabo las ceremonias rituales ordinarias. Este “lugar santo” (heb. hékal, palabra derivada, a través del cananeo, del sumerio E. GAL, ‘casa grande’) medía 40 codos de longitud, 20 de anchura, y 30 de altura. Puertas dobles de madera de ciprés lo separaban del pórtico, y cada puerta se componía de dos hojas.”»[1]
El Templo de Jerusalén tal como lo imaginó un teólogo alemán del siglo XVI. Las seis torres, el frontón triangular clásico, las dos columnas exentas coronadas con esferas tienen su contrapartida en esta imagen de como pudo ser El Escorial en las primeras fases del proyecto
II.Comentarios sobre Matemáticas
Haremos un breve repaso histórico de Matemáticas. El número pi es número matemático, de tipo real, ya que contiene decimales. Su importancia de conocer de la historia de este número es ver si el autor del mar de bronce, construido en el interior del templo, conocería o no los números reales, ya que como vemos, se utilizó un valor exacto (Pi=3) y se obviaron los decimales.
a.¿Quien descubrió los números reales?
«Los egipcios utilizaron por primera vez las fracciones comunes alrededor del año 1000 a. C.; alrededor del 500 a. C. el grupo de matemáticos griegos liderados por Pitágoras se dio cuenta de la necesidad de los números irracionales. Los números negativos fueron inventados por matemáticos indios cerca del 600, posiblemente reinventados en China poco después, y no se utilizaron en Europa hasta el siglo XVII, si bien a finales del XVIII Leonhard Euler descartó soluciones negativas para las ecuaciones porque lo consideraba irreal. En ese siglo, en el cálculo se utilizaba un conjunto de números reales sin una definición concisa, cosa que finalmente sucedió con la definición rigurosa hecha por Georg Cantor en 1871.
En realidad, el estudio riguroso de la construcción total de los números reales exige tener amplios antecedentes de teoría de conjuntos y lógica matemática. Fue lograda la construcción y sistematización de los números reales en el siglo XIX por dos grandes matemáticos europeos utilizando vías distintas: la teoría de conjuntos de Georg Cantor (encajamientos sucesivos, cardinales finitos e infinitos), por un lado, y el análisis matemático de Richard Dedekind (vecindades, entornos y cortaduras de Dedekind). Ambos matemáticos lograron la sistematización de los números reales en la historia no de manera espontánea, sino echando mano de todos los avances previos en la materia: desde la antigua Grecia y pasando por matemáticos como Descartes, Newton, Leibniz, Euler, Lagrange, Gauss, Riemann, Cauchy y Weierstrass, por mencionar sólo a los más sobresalientes.»[2]
b. Historia de Pi [3]

b.0. Referencias bíblicas a Pi
Una de las referencias documentadas más antiguas al número pi se puede encontrar en un versículo poco conocido de la Biblia
I Re. 7:23:RV 1960 “Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos.”
Se puede ver cómo una idea similar se puede encontrar en II Crónicas 4:2.
“También hizo un mar de fundición, el cual tenía diez codos de un borde al otro, enteramente redondo; su altura era de cinco codos, y un cordón de treinta codos de largo lo ceñía alrededor.”
En él aparece en una lista de requerimientos para la construcción del Gran Templo de Salomón, construido sobre el 950 a. C. y su interés aquí radica en que da un valor de π = 3,0.
b.1.Época egipcia
El uso del número π en las culturas antiguas se remonta al que hacía el escriba egipcio Ahmes en el año 1800 a. C., descrito en el papiro de Rhind, donde se emplea un valor de π afirmando que el área de un círculo es similar a la de un cuadrado cuyo lado es igual al diámetro del círculo disminuido en 1/9, es decir igual a los 8/9 del diámetro. Es decir que:

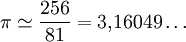
Entre los ocho documentos matemáticos de la cultura egipcia hallados hasta hoy, en sólo dos se habla de círculos. Uno es el papiro de Rhind y el otro es el papiro de Moscú. Sólo en el primero se habla del cálculo del número π. El investigador Otto Neugebauer, en un anexo de su libro «The Exact Sciences in Antiquity», describe un método supuestamente inspirado por los problemas del papiro de Ahmes para averiguar el valor aproximado de π mediante aproximación a un cuadrado de lado 8/9 del diámetro.
Algunos matemáticos mesopotámicos empleaban en el cálculo de segmentos valores de π iguales a 3, alcanzando en algunos casos valores más refinados de 3 y 1/8.
b.2.Época griega

Método de Arquímedes para encontrar dos cotas que se aproximen al número π.
El matemático griego Arquímedes (siglo III a. C.) fue capaz de determinar el número π entre el intervalo comprendido por 3 10/71, como valor mínimo y 3 1/7, como valor máximo. Con esta aproximación de Arquímedes se obtiene un valor con un error que oscila entre 0,024% y 0,040% sobre el valor real. El método empleado por Arquímedes era muy simple y consistía en circunscribir e inscribir polígonos regulares de n-lados en circunferencias y calcular el perímetro de dichos polígonos. Arquímedes empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.
En el siglo II, Claudio Ptolomeo proporciona un valor fraccionario por aproximaciones:

b.3.La matemática persa y china
El cálculo de pi fue una atracción para todas las culturas con matemáticos dedicados, de esta forma se tiene que el matemático chino Liu Hui fue el primero en sugerir que 3,14 era una buena aproximación, usando un polígono de 96 lados. Posteriormente estimó π como 3,14159 empleando un polígono de 3072 lados.
En el siglo V, el matemático y astrónomo chino Zu Chongzhi calculó π en 3,1415926 al que llamo «valor por defecto» y 3,1415927 «valor por exceso», y dio dos aproximaciones racionales de π: 22/7 y 355/113 muy conocidas ambas, siendo la ultima aproximación tan buena y precisa que no fue igualada hasta 900 años después, en el siglo XV
En el siglo XV, el matemático persa Ghiyath al-Kashi fue capaz de calcular π con 9 dígitos empleando una base numérica sexagesimal, lo que equivale a una aproximación de 16 dígitos decimales: 2π = 6,2831853071795865.
b.4.Renacimiento europeo


John Wallis, (1616–1703)

Leonhard Euler, (1707–1783)
A partir del siglo XII, con el uso de cifras arábigas en los cálculos, se facilitó mucho la posibilidad de obtener mejores cálculos para π. El matemático Leonardo Pisano, en su «Practica Geometriae», amplifica el método de Arquímedes, proporcionando un intervalo más estrecho. Algunos matemáticos del siglo XVII, como Vieta, usaron polígonos de hasta 393.216 lados para aproximarse con buena precisión a 3,141592653.
El matemático inglés John Wallis desarrolló en 1655 la conocida serie Producto de Wallis:
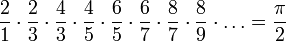
De la misma forma Leibniz calculó de una forma más complicada en 1682 la siguiente serie que lleva su nombre:
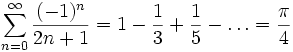
b.5.Época moderna (pre-computacional)
Fue en el año 1706 cuando el galés William Jones afirmó «3,14159 andc. = π». Leonhard Euler adoptó el conocido símbolo en 1737 e instantáneamente se convirtió en una notación estándar hasta hoy en día.
En 1610 el matemático Ludolph van Ceulen calculó los 35 primeros decimales de π. Se dice que estaba tan orgulloso de esta hazaña que lo mandó grabar en su lápida. Los libros de matemática alemanes durante muchos años denominaron a π como número ludofiano.
El matemático japonés Takebe empezó a calcular el número π en el año 1722 con el mismo método expuesto por Arquímedes, y fue ampliando el número de lados para polígonos circunscritos e inscritos hasta llegar a 1.024 lados. Este ingente trabajo consiguió que se determinara π con 41 decimales.
Johan Heinrich Lambert(1728-1777), matemático alemán, probó que Pi es irracional. (Un número irracional no se puede escribir en forma de fracción racional. Números racionales son : 1, 2 , 3/4, 17/23)» [4]
En 1789 el matemático de origen eslovaco Jurij Vega, mediante la fórmula de John Machin descubierta en 1706, fue el primero en averiguar los primeros 140 decimales de π, de los cuales 126 eran correctos; este récord se mantuvo durante 52 años, hasta que en 1841 William Rutherford calculó 208 decimales de los cuales 152 eran correctos.
El matemático aficionado de origen inglés William Shanks consumió cerca de 20 años de su vida calculando π con 707 decimales (evento acaecido en 1873). En el año 1944, D. F. Ferguson encontró un error en la posición decimal 528, a partir del cual todos los dígitos posteriores eran erróneos. En 1947, Ferguson recalculó π con 808 decimales con la ayuda de una calculadora mecánica.
b.6.Época moderna (computacional)

Desde el diseño de la primera computadora se empezaron a desarrollar programas para el cálculo del número π con la mayor cantidad de cifras posibles. De esta forma, en 1949 un ENIAC fue capaz de romper todos los récords del momento con 2037 lugares decimales (en 70 horas). Poco a poco se fueron sucediendo los ordenadores que batían récords, y de esta forma pocos años después (1954) un NORAC llegó a 3092 cifras. Durante casi toda la década de los años 1960 los IBM fueron batiendo récords, hasta que un IBM 7030 pudo llegar en 1966 a 250.000 cifras decimales (8 h y 23 min). Durante esta época se probaban las nuevas computadoras con algoritmos para la generación de series de números procedentes de π.
Ya en la década de 2000, los ordenadores eran capaces de sacar cifras récord inmensamente grandes; en 2004 fueron capaces de sacar 1,3511 billones de lugares decimales mediante el uso de una supercomputadora Hitachi, que llegó a trabajar sólo 500 horas para realizar el cálculo.
Año 1949 Descubridor Ordenador utilizado Número de cifras decimales
G.W. Reitwiesner y otros
ENIAC
2.037
1954
NORAC
3.092
1959
Guilloud
IBM 704
16.167
1967
CDC 6600
500.000
1973
Guillord y Bouyer
CDC 7600
1.001.250
1981
Miyoshi y Kanada
FACOM M-200
2.000.036
1982
Guilloud
2.000.050
1986
Bailey
CRAY-2
29.360.111
1986
Kanada y Tamura
HITAC S-810/20
67.108.839
1987
Kanada, Tamura, Kobo y otros
NEC SX-2
134.217.700
1988
Kanada y Tamura
Hitachi S-820
201.326.000
1989
Hermanos Chudnovsky
CRAY-2 y IBM-3090/VF
480.000.000
1989
Hermanos Chudnovsky
IBM 3090
1.011.196.691
1991
Hermanos Chudnovsky
2.260.000.000
1994
Hermanos Chudnovsky
4.044.000.000
1995
Kanada y Takahashi
HITAC S-3800/480
6.442.450.000
1997
Kanada y Takahashi
Hitachi SR2201
51.539.600.000
1999
Kanada y Takahashi
Hitachi SR8000
68.719.470.000
1999
Kanada y Takahashi
Hitachi SR8000
206.158.430.000
2002
Kanada y otros
Hitachi SR8000/MP
1.241.100.000.000
2004
Hitachi
1.351.100.000.000

En la época computacional del cálculo de π las cifras se han disparado, no sólo debido a la potencia de cálculo que estas máquinas son capaces de generar, sino también por el prestigio que conlleva para el constructor de la máquina el que su marca aparezca en la lista de los récords.
II. Construcción del Templo del rey Salomón
«El Rey Salomón acababa de terminar el Templo cuando se dispuso a construir un palacio para él y su corte. Tardó trece años en construirlo, y la Biblia cuenta con bastante lujo de detalles cómo llevó acabo su proyecto. Los pórticos, las columnas, los capiteles, las fuentes… pero hay un elemento en particular que es de interés matemático.

Letra griega pi. Símbolo adoptado inicialmente en 1706 por William Jones y popularizado por Euler.
Ver Temas relacionados con Pi
HISTORIA DEL NÚMERO PI
Algunas curiosidades sobre el número Pi (pi)
Dice así el texto sagrado:
I Reyes 7:23
RV 1960 “Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos.”
RV 1909 “Hizo asimismo un mar de fundición, de diez codos del un lado al otro, perfectamente redondo: su altura era de cinco codos, y ceñíalo alrededor un cordón de treinta codos.”
NVI “Hizo también una fuente circular de metal fundido, que medía cuatro metros y medio de diámetro y dos metros con veinticinco centímetros de alto. Su circunferencia, medida a cordel, era de trece metros y medio.”
RV 1995 “Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo. Tenía cinco codos de altura y a su alrededor un cordón de treinta codos.”
LBLA “Hizo asimismo el mar de metal fundido de diez codos de borde a borde, en forma circular; su altura era de cinco codos, y tenía treinta codos de circunferencia.”
Reina-Valera Antigua “Hizo asimismo un mar de fundición, de diez codos del un lado al otro, perfectamente redondo: su altura era de cinco codos, y ceñíalo alrededor un cordón de treinta codos.”
Este “mar” al que se está refiriendo el texto es un monumental cuenco de bronce parecido al que vemos en la imagen. La altura, 5 codos, es el único dato que no nos interesa. Lo demás sí:
1. Es “perfectamente redondo” (una circunferencia).
2. Tiene “diez codos de un lado al otro” (diámetro = 10 codos)
3. “Lo ceñía un cordón de treinta codos” (longitud de la circunferencia = 30 codos)
Recordemos que el número pi se obtiene de dividir la longitud de la circunferencia entre el diámetro. En este caso pi = 30/10 = 3. Sin decimales, 3 es una aproximación bastante burda si la comparamos con la retahíla de 3,141592… que todos conocemos de la primaria. Pero para el tiempo de Salomón (sobre el 950 a.C), y en sintonía con su aclamada sabiduría, era una medición exquisita.
Sin embargo no era la primera medición expresa del misterioso número. Los Egipcios dieron con un valor de 25/8 = 3,125. No está nada mal. Los Mesopotámicos asemejaron pi al valor de la raíz cuadrada de 10, que es 3,162. La historia de cómo llegaron a esta comparación sobrepasa el presente artículo, pero es bien interesante.
Escultura de Pi en la ciudad de Seattle
En defensa de los peritos de Salomón cabe decir que la “perfecta redondez” de semejante chisme probablemente no era tan fácil de conseguir. También hay quien defiende que el cuenco tenía un borde grueso de forma que el diámetro se midió para el borde interior, mientras que la longitud de la circunferencia se midió para el borde exterior, dando el dando el error de pi que observamos.
En cualquier caso fue el comienzo de una serie de aproximaciones a pi seguidas por la primera aproximación teórica (de Arquímedes), luego Ptolomeo, el chino Zu Chongzhi, los árabes al-Khwarizmi y al-Kashi, y seguida finalmente por numerosos europeos del Renacimiento y la Ilustración que consiguieron aproximadamente los primeros 500 dígitos de pi.

Hoy en día los ordenadores se han convertido en herramienta fundamental para el cálculo de pi. Se han calculado con éxito un total de 51000 millones de decimales. Sin embargo el afamado número sigue sin querer contarnos todos sus secretos, a la vez que nos plantea nuevas incógnitas.
Cada 14 de Marzo (3/14 según el calendario sajón) se celebra el día de pi. Para los más frikis (neologismo que galopante se abre paso entre nosotros, y que denota a los fanáticos de aficiones no destructivas pero sí extravagantes) no sólo se celebra el día, sino el momento de pi: El 14 de Marzo a la 1 de la mañana, 59 minutos y 26 segundos, que todo junto nos da 3,1415926.
Rarezas aparte, estamos ante un estudio de milenios de edad que todavía sigue sorprendiéndonos, y que hemos conseguido relacionar con muchas disciplinas. Peter Borwein lo resume de forma magistral: “Hay una belleza en pi que nos hace seguir mirándolo… Los dígitos de pi son extremadamente aleatorios. No tienen ningún patrón, y en matemáticas eso es lo mismo que decir que tiene todos los patrones”. Por eso precisamente es tan fascinante.»[5]
En 1 Reyes 7:23, hablando del Templo de Salomón dice:
”Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos.”
Pablo Hoff comenta que «La obra de arte del mar de fundición,(el pilón de agua lustral,ubicado en el atrio),era meramente de adorno»[6]
Pero aparentemente tenía un simbolismo:
«Este enorme mar parece simbolizar el gran mar cósmico, que era para los antiguos la fuente de la vida y la fecundidad. Su uso estaba reservado exclusivamente a los sacerdotes, para diversos tipos de purificaciones. En 2 R 16.17; 25.13 se habla del fin que tuvo esta bella obra de arte.»[7]
Ver Pesos y medidas usados en la biblia
¿Está equivocada la Biblia?
«…el mar de bronce del que habla, es, en realidad, un cilindro, con altura de cinco codos, que a nuestros efectos es irrelevante, pero el diámetro es de diez codos, por tanto, si la circunferencia es de 30 codos, tenemos que el valor de pi vale 3.
Además, es imposible lo que dice, pues el valor de la circunferencia sería 31,4 codos, por lo que un cordón de 30 codos nunca podría ceñir el cilindro, se quedaría corto. Debería ser, al menos, 32 codos.
No creo que haya que saber muchas matemáticas, en general una sencilla aproximación basta siempre para las cosas diarias.
El problema es que el valor de pi era conocido 700 años antes en Babilonia y en Egipto, por lo que, siendo la biblia un libro inspirado por Dios debe, al menos, reflejar los conocimientos de la época. Reflejar menos implica que eran unos ignorantes los redactores, lo cual no se lleva muy bien con la inspiración divina.
Un cordón de 30 codos (o lo que sea) no puede ceñir un cilindro de 10 codos de diámetro, es sencillamente imposible…
El cordón medía 30 codos porque ceñía al mar semiesférico bastante por debajo del borde.
Recuerda que el mar fundido en realidad era como una especie de media naranja (perfectamente redondo, según 1 Reyes 7: 23), con el borde formando algo así como una flor de lirio, un detalle decorativo, luego venían por debajo 2 hileras de calabazas. Muy probablemente la soga o cordón bordeaba por debajo de las calabazas, pero es un detalle menor, ya que no necesariamente.¿Entiendes? Nadie está negando que el valor de Pi sea el que es y que tan bien conocían los babilonios y egipcios, y seguramente también los hebreos por el contacto cultural con estas civilizaciones.
El asunto es la ubicación de la soga, que no habría estado en la línea media, sino unos centímetros más abajo, OK?
Fíjate en el esquema que te envío, analízalo bien. Exageré quizás el emplazamiento de la soga para que se entienda mejor lo que te comenté.
La verdad es que con las traducciones, supongo que se pierde el sentido original, no obstante, si fuese esta la solución carece de sentido dar las medidas del cordón que ciñe, ¿por qué no 20 o 25?, pues depende de donde se coloque.
Lo lógico es dar una medida con significado, y la única es la del borde exterior.
A mi me sigue pareciendo más lógica la explicación de que refleja los conocimientos de la época, y los redactores, hebreos de la edad del bronce, tenían unos conocimientos limitados, por supuesto inferiores a Babilonia o Egipto. En general, en los libros de historia de las matemáticas se adopta este criterio, y se mantiene que la aproximación de la Biblia al valor de pi es 3.
En cualquier caso la explicación, al menos, parece plausible.

Si consideramos el dibujo propuesto como una semiesfera tenemos que el Volumen se calcula con
V=2/3 * pi * R3 (R3 = Radio al cubo)
Considerando el codo de 45cm o 0.45m
El Radio es de 5 codos, o sea 2.25m
V=2/3*3.14*2.25*2.25*2.25=23.844 metros cubicos o sea 23844 litros
Tomando el bato de 22 litros (el mas chico que encontre ya que varia hasta 37 litros)
22384/22=1084 batos
Ahora considerándolo cilíndrico (lo que descarta el dibujo propuesto) el tenemos V=pi*R2*h (R2=radio al cuadrado)
La altura es de 5 codos, o sea 2.25 m
V=3.14*2.25*2.25*2.25=35.766 metros cúbicos o sea 35766 litros
En batos=1625
Esto es considerando el borde externo y que esta lleno hasta el tope
Por lo tanto no entran los 2000 batos indicados en Reyes y menos los 3000 indicados en 2 Crónicas.
Quizás las medidas de los codos y los batos están mal….. Quizás
A ver. Saquemos los cálculos del medio.
Reyes 7:23 Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos.
Pi es la relación entre la longitud de la circunferencia y su diámetro. En este caso el cordón que mide 30 codos /10 codos = 3 y no 3,14159….. Esto significa que el cordón no alcanza a rodear el recipiente.
La solución posteada por Migdol es la de un recipiente con forma de una semiesfera (como una pelota partida al medio) y colocar el cinturón por debajo del borde superior a una altura donde la circunferencia mida 30 codos y hacer aparecer el número pi.
El problema de esta solución es que esta forma disminuye considerablemente la capacidad del recipiente y según Reyes 7:26 …y cabían en él dos mil batos. (aprox 44000 litros)
El recipiente semiesférico solo puede contener 24000 litros
Otra solución podría ser la del dibujo donde el borde superior tiene los 10 codos de diámetro pero el problema sigue siendo el volumen del recipiente, en este caso 36000 litros.
El otro tema es que en 2 Crónicas 4:5 dice … Y le cabían tres mil batos (aprox 66000 litros)
O sea que a pi lo podemos hacer aparecer ya que la descripción es muy imprecisa. Lo que no podemos es almacenar la cantidad de liquido indicada.
El valor de pi=3 no está tan mal para la época. Lo babilonios por aquel entonces pensaban que pi era tres. Pero los egipcios unos siglos antes ya habían ido más lejos al expresar a pi como (4/3)^4=3,16. Pero es estéril la discusión con cualquier fanático. te pondrá la cuerda dónde le interese.» [8]
Críticas a la geometría
En el portal sindioses, encontré un artículo muy gracioso, escrito con muy buen sentido del humor, sobre este tema, de Pi=3 «En la Biblia se afirma que pi vale 3 (1 Reyes 7:23), por lo que debemos enseñarlo así en los cursos de geometría para que sean correctos, ¿por qué cree usted hermano, que los edificios no soportan los terremotos? ¡Porque no los fabrican con el verdadero valor de pi!!!!!. Si los fabricaran con un valor de pi igual a tres, las construcciones ganarían solidez debido a la gracia divina que los protegería de todo mal basados en que el tres ¡es el numero de la Trinidad! Y por la gracia de las Tres Personas los edificios quedarían protegidos contra todo mal. Además, el valor actual de pi es un numero feo, difícil de recordar y ¡aproximado!, si amigo lector, es verdad, ellos no quieren que se sepa pero es verdad, el valor real que ellos consideran de pi es desconocido ¿cómo pueden estos que nos hablan de ciencia decir que sus matemáticas son exactas si ni siquiera conocen el valor de este número? ¿Cómo pueden construir cosas sólidas si no tienen precisión al medir?. En cambio Dios en su infinita sabiduría lo hizo exactamente igual a tres para que no hubieran aproximaciones y pudiera ser exacto y justo todo lo que es circular, amén hermanos que les hablo como me fue revelado y el hecho de que pi valga 3 es una hermosa prueba de que Dios existe y es trino, así lo nieguen los ciegos de mente cerrada que no ven más allá de sus narices y son incapaces de romper sus dogmas. ¡Alabado sea el señor por toda la eternidad! » [9]
En respuesta a esta críticas escrita en un bueno y sano sentido de humor, mas allá de que en el fondo es un crítica, creo que es importante responder este tema mirando a Jesús, quien en su época fue confrontado por una persona muy astuta e inteligente quien le preguntó sobre si estaba bien pagar los impuestos al gobierno de esa época; hoy también muchos preguntan y cuestionan con astucia sobre si la participación cívica, social y política de los cristianos es correcta. O si debemos enseñar ciencia en las aulas o religión a los alumnos.
La respuesta de Jesús (Lucas 20:25) debe ayudarnos a dar la nuestra hoy. Jesús respondió: “Dad a César lo que es de César, y a Dios lo que es de Dios.”
Si leemos bien la respuesta que Jesús dio a esa persona de sus días, nos daremos cuenta que el Maestro no negó la existencia del Estado y sus reglas relacionadas con los impuestos, sino que animó a los oyentes a ser responsables tanto con el Estado como con Dios. Y lo mismo podemos decir con respecto a las enseñanzas de la ciencia. Después de todo, los seguidores de Cristo creemos que Dios es soberano sobre todo y en todos. Si las autoridades del pais en el que nos toca vivir determinan un plan de enseñanza, los cristianos debemos respetarlo, aunque no nos guste o no estemos de acuerdo en lo que respecta a nuestra fe.
Si el gobierno nos prohibiera creer en Cristo, bueno, ahí sí se terminó la obediencia.Pero en este tema, no veo ninguna agresión a la fe cristiana ni ninguna necesidad de afirmar que Pi=3, cuando tampoco la biblia lo enseña.Repito lo que ya he comentado, es tan solo una narración histórica de como fue construido el templo del rey Salomón y no una discusión matemática sobre la superioridad de un valor sobre otro.
Pero si la ciencia hoy en dia ha determinado que Pi=3,1416…, y eso es lo que se enseña en las escuelas, pues hay que estudiar lo que se enseña, ya que esto no afecta nuestra fe cristiana en absoluta.
Además, tampoco el pasaje bíblico en cuestión está realizando una apologética o defensa de la superioridad de un valor matemático sobre otro. Simplemente está narrando los hechos relacionados con la construcción del templo de Salomón.

Pi = 3. ¿Lo pone en la Biblia?
«7:23 Él hizo además el Mar de metal fundido, que medía cinco metros de diámetro y tenía forma circular; su altura era de dos metros y medio, y una cuerda de quince metros medía su circunferencia.
Para aquellos que no recuerdan muy bien como calcular el número Pi, o sea este π, vamos a ponerlo de forma simple.
Bien pues π = 3.141592… ya que si tuviéramos una cuerda alrededor de una circunferencia de diámetro 1, la cuerda tendría una longitud de 3.141592…, para que lo veáis de forma más gráfica.
Bien, pues la proporción de las sagradas escrituras es que el diámetro = 5 por lo que echando unos cálculos simples llegamos a la conclusión de que la cuerda que medía su circunferencia debería ser igual a… 15.70… Pero no, es 15, ni más ni menos, y como esta en las sagradas escrituras pues…
Ah, es verdad, no recuerdo que ningún cristiano radical halla puesto en duda que Pi = a 3.141592, es más, seguramente digan que es un error de traducción o que sea simplemente una historia narrativa representativa y que no se tienen que tomar en cuanta lo números… Entonces por qué se ceban en creer que el creacionismo , porque no lo ven como una historia narrativa representativa del poder divino, y sí como el comienzo de la historia de la humanidad.
Como bien dice el artículo. Si Dios hizo al hombre porque lo pone en la Biblia, π = 3 por la misma razón. Es lo que tiene creer en algo tan fuera de lugar, que o todo o nada.»[10]
Ver La Biblia (I)
HIRAM
Hiram ensena los planos a Salomon.
Grabado de J.J. Scheuchzer
"Physica Sacra Iconibus Illustrata"
Ausburgo, 1731
Nombre del «artífice a quien el rey de TIRO, del mismo nombre, envió a Salomón para que hiciese las decoraciones en bronce del templo (1 R 7.13–47; 2 Cr 2.13, 14; 4.11–18). Era hijo de un artífice de Tiro y de una mujer israelita, quizás de la tribu de Neftalí (1 R 7.14) o de la de Dan (2 Cr 2.14). Su principal obra en el templo fueron las dos grandes columnas que recibieron los nombres de Jaquín y Boaz.»[11]
I Reyes 7:23 ” hijo de una viuda de la tribu de Neftalí. Su padre, que trabajaba en bronce, era de Tiro; e Hiram era lleno de sabiduría, inteligencia y ciencia en toda obra de bronce. Este, pues, vino al rey Salomón, e hizo toda su obra.”
Hiram era un experto en el tema de trabajar en bronce. Además, su padre estaba en el mismo oficio, lo que nos muestra que seguramente fue su padre quien el enseño el oficio. No era un ignorante en e oficio del bronce construcción. Su madre era una mujer israelita, seguramente una mujer piadosa.
«Este técnico, fue recomendado por el rey de TIRO, del mismo nombre, Hiram, quien fue un gran admirador de David (1 R. 5.1), y le envió materiales y artesanos para que ayudaran en la construcción de su palacio en Jerusalén (2 S. 5.11; 1 Cr. 14.1)
Cuando Salomón ascendió al trono Hiram envió emisarios para hacer nuevos contactos, los que condujeron a un tratado comercial por medio del cual enviaba madera del Líbano y artesanos calificados para la construcción del nuevo templo en Jerusalén, a cambio de un pago anual, por parte de Salomón, de trigo y aceite (1 R. 5.2-11), que faltaban en las ciudades fenicias. Aparentemente requirió pagos adicionales de cebada y vino para el mantenimiento de los obreros tirios, que incluían técnicos familiarizados con el diseño y el teñido de telas, y que fueron enviados para instruir a los israelitas (2 Cr. 2.3-7).
[…]
Tratados semejantes, para reajustar las fronteras entre los estados, se conocen por acuerdos sirios primitivos (p. ej. Alalak).
[…]
Flavio Josefo
Aparte del AT hay una crónica del gobierno de Hiram escrita por Flavio Josefo (Ant. 8. 50-54; Contra Apionem 1. 17s) basada en los historiadores Menandro y Dío. Según esta fuente, Hiram (lxx Jiram, gr. Heiramos, Heirómos) era hijo de Abi baal, y reinó 34 años hasta su muerte a la edad de 53. La construcción del templo de Jerusalén comenzó en el 11º año de su reinado, e. d. el cuarto de Salomón (1 R. 6.1).
[…]
Josefo, al igual que Eupólemo y Alejandro Polihistor, habla de las cartas, que según se dice fueron guardadas en los archivos estatales de Tiro, que se escribieron Hiram y Salomón con motivo de la construcción del templo. También afirma Josefo que los dos reyes intercambiaron acertijos, hasta que Salomón fue derrotado por un joven tirio llamado Abdemón. Clemente de Alejandría y Taciano dicen que una hija de Hiram se casó con Salomón; cf. la declaración de que entre sus esposas se encontraban algunas sidonias (IR.11:1-2).»[12]
Ver HIRAM, EL ARQUITECTO DEL PRIMER TEMPLO
En el portal Se nos va de las manos…,realiza una crítica sobre los que utilizan la Biblia con fines cabalísticos, para proponer fechas del advenimiento de Cristo, o para mostrar que hay números escondidos en la Biblia.
«Los fundamentalistas generalmente se basan en la supuesta inspiración de los textos bíblicos para tratar de “profetizar” eventos futuros. Todo esto se hace bajo la segura guía de las cifras “inspiradas” que aparecen en la Biblia. El ejemplo más diáfano de esto es la forma como las diversas sectas de corte pentecostal y adventista se jactan de contar años y generaciones bíblicas para tratar de anticiparse al fin de este “sistema de cosas” o incluso, los evangélicos preparándose al “arrebatamiento” que supuestamente experimentarán los hijos de Dios en el fin del mundo.
No hay tiempo más desperdiciado que el que se gasta en estos cálculos, pues como mostraré con diversos ejemplos, nos daremos cuenta de que los “números” que aparecen en la Biblia no suelen ser más que cifras ridículas, inventadas torpemente por los redactores ya fueran judíos o cristianos.
[...]
¿Qué consecuencia trae la aparición de este error en la Biblia, para los ingenuos fundamentalistas que tratan de averiguar en las supuestas profecías la fecha del fin del mundo ?
Es simple. Los fundamentalistas están tratando con cifras del orden de 5000 años para sus torpes cálculos apocalípticos. Un error de un 6% en estos cálculos arroja una incertidumbre de cerca de 300 años.
Es decir, si un “estudioso” bíblico dice que la profecía bíblica arroja una fecha para la venida de Jesucristo de 1914, en realidad debería agregar la incertidumbre asociada; si llamamos Ta al tiempo del arrebatamiento o Tc al tiempo de inicio del reinado de Cristo, un fundamentalista debería decir algo como :
Ta = 1999 ± 600 años
Y un testigo de Jehová debería decir
Tc = 1914 ± 600 años.
¿Cómo sería la urgencia en la predicación si los testigos de Jehová fueran honestos y dijeran: “¡El tiempo está cerca… antes de 600 años empieza la batalla de Armagedón!”? ¿O si los evangélicos tuvieran que decir, “antes de 600 años seremos arrebatados por los cielos”?
Desde esta óptica es comprensible el por qué los cristianos llevan esperando en vano desde hace 2000 años, cual mansos borregos, la “Inminente (¡!) Segunda venida” de “Nuestro Señor” Jesucristo. Es comprensible también, por qué el “Siervo fiel y Discreto” (Los Estafadores Testigos de Jehová de Brooklin) hayan recibido la luz de la llegada del fin, en cerca de 5 ocasiones, y siempre hayan sido fechas erróneas. Los cristianos seguirán esperando el fin del mundo tal como lo llevan haciendo durante 2000 años por una razón muy simple… El fin nunca llegará.”»[13]
La replica a esta crítica es sencilla.El día y la hora de su retorno no lo conoce nadie. Jesús, en los tiempos de su humanidad también negó conocer ese momento. Es verdad que no debemos poner fecha y hora, y todos los que han puesto fecha han fallado.Pero el dijo que debíamos velar y orar para evitar caer en tentación antes de su venida. También esta el ejemplo (parábola) de las vírgenes insensatas, que no tuvieron sus lámparas llenas de aceite y cuando el novio vino se habían quedad dormidas y no pudieron celebrar la llegada del novio (Cristo)
Conclusión:
a. Respecto de Pi=3
Es probable que los hebreos no conocieran los decimales.Sin embargo hay algunos interrogantes que todavía no tengo respuesta:
a.1. Posibles respuestas
Un comentarista de un foro, comenta que:
«La Biblia se debe entender literalmente, pero debe ser leída con atención, y no hacerle decir lo que no dice….ni falla la inspiración divina. En este caso, hay que notar dos cosas por lo menos:
El cordón de 30 codos que ceñía la fuente alrededor, en ninguna parte dice que estaba justo en el borde superior.
La fuente tenía una forma semiesférica, y si este cordón estaba más abajo del borde, la circunferencia puede tener exactamente 30 codos, aunque el diámetro superior sea de 10 codos, al descender es menor.
a.2. En este caso, hay que notar dos cosas por lo menos:
1. El cordón de 30 codos que ceñía la fuente alrededor, en ninguna parte dice que estaba justo en el borde superior. La fuente tenía una forma semiesférica, y si este cordón estaba más abajo del borde, la circunferencia puede tener exactamente 30 codos, aunque el diámetro superior sea de 10 codos, al descender es menor.
2. Otra forma de aproximarse al problema es reconocer que pi es un número irracional, con infinitas cifras decimales no periódicas, lo cual hace que cualquier forma de escribirlo sea tan sólo una aproximación. Nunca se puede escribir de manera exacta, pero esto no quiere decir que sea erróneo, sino que depende del uso que se le dé al dato.
Se puede escribir 3,14; 3,1416; 3,14159265; etc. En este caso, decir que es sencillamente 3 es una buena aproximación para los fines descriptivos del texto, que se refiere a los muebles del Templo.»[14]
El valor de Pi cambia en las distintas culturas
«En el antiguo Egipto pi se consideraba como 3,1605, sin embargo en la antigua Babilonia era considerado como 3. Si hacemos un recorrido por la historia veremos que el número pi tenía un valor distinto para muchos de los pueblos y culturas» [15]

«Parece que fue W. Jones el primero que empleó la letra griega pi para designarlo en su libro “Introducción a las matemáticas” (1.706), por ser la inicial de la palabra periferia (circunferencia).
Los egipcios ya conocían que la relación entre el diámetro y la longitud de una circunferencia no se podía calcular con exactitud y la expresaron con 3 + 1/6 ó 3,16.
Muchos siglos después el gran Arquímedes de Siracusa diseñó el método de los polígonos inscritos y circunscritos para calcularlo, que comentaré más adelante.
Así obtuvo el valor de pi = 3 + 1 / 7 ó 22 / 7 = 3,1428
Ptolomeo calculó que pi = 3 + 1 / 8 + 1 / 60 = 3,14166
Los matemáticos árabes y chinos habían hallado que pi era igual a 3,1416
Este procedimiento estuvo vigente hasta el siglo XVII, a partir de aquí los matemáticos comenzaron a diseñar algoritmos de cálculo, en los que no interviene la circunferencia, cada vez más originales y eficientes y los progresos fueron relativamente rápidos, yo destacaría algunos como:
p = 2 x 2 x 4 x 4 x 6 x 6 x… Algoritmo de Wallis
2 3 x 3 x 5 x 5 x 7 x 7 x…
p = 1 + 1 + 1 +… Algoritmo de Leibniz
8 1 x 3 5 x 7 9 x 11
p2 = 1 + 1 + 1 + 1 +… + 1, o sea, p2 = 6 · S (1/n2) Algoritmo de Euler
6 4 9 25 n2

Así el número de decimales hallados de pi fue aumentando sin parar:
Van Ceule encontró 35 que hizo grabar en su tumba.
Sharp halló 72, Lagny: 127, Vega: 139, Rutherford llegó a los 208 en 1.841 y a 440 en 1.872, pero el británico William Shanks, que dedicó 20 años de su vida, estableció la última gran marca de los calculistas, digamos manuales, al llegar al decimal 707 en 1.874. Fue homenajeado como un héroe y se escribieron bajo la cúpula del palacio de la Découverte de Paris.
Desgraciadamente en el año 1.947, D. F. Ferguson descubrió que el decimal 528 era incorrecto, y obviamente todos los siguientes…
A partir de la década de los 40, la aparición de los ordenadores ha permitido profundizar, rápidamente, en el cálculo de pi, así en 1.949 se llegó a los 2.036 decimales, en 1.959 ya eran 10.000, en 1.974 se consiguieron obtener 1.000.000. Uno de los últimos récords sobrepasaba los 6 mil millones en 1.995.
Aquí tenéis, a título informativo, los 100 primeros decimales de pi que, obviamente, no aplicaréis en vuestros problemas geométricos, pero que siempre son curiosos de ver e, incluso, os pueden servir de entrenamiento memorístico. ¿Os atrevéis?
pi = 3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679…» [16]
«William James, Filósofo estadounidense, dijo dos cosas muy interesantes:
1 “Los decimales no calculados de pi, duermen en un misterioso reino abstracto, donde gozan de una débil realidad, hasta que no son calculados, no se convierten en algo plenamente real, e incluso entonces su realidad es mera cuestión de grado.”
2 “Si consideramos el mundo de relaciones geométricas, allí duerme el milésimo decimal de Pi, aunque jamás nadie trate de calcularlo.” » [17]
Me pregunto, que sentido tiene buscarle el milésimo decimal al número Pi, si no lo vas a usar. Así tiene que haber sido en el diseño y construcción del mar de bronce. Uso Pi=3 por dos razones posibles:
1. Tomó el modelo babilónico, que a lo mejor era el que el diseñador (Hiram) conocía.
2. o simplemente no necesitó los decimales por alguna razón que no se comprende bien.
Recordemos que Hiram era un hombre sabio, y conocía su oficio perfectamente bien.Y que como ya dijimos venia recomendado por el rey, como un hombre sabio que conocía muy bien su trabajo:
“Entonces Hiram rey de Tiro respondió por escrito que envió a Salomón: Porque Jehová amó a su pueblo, te ha puesto por rey sobre ellos. Además decía Hiram: Bendito sea Jehová el Dios de Israel, que hizo los cielos y la tierra, y que dio al rey David un hijo sabio, entendido, cuerdo y prudente, que edifique casa a Jehová, y casa para su reino. Yo, pues, te he enviado un hombre hábil y entendido, Hiram-abi, hijo de una mujer de las hijas de Dan, mas su padre fue de Tiro; el cual sabe trabajar en oro, plata, bronce y hierro, en piedra y en madera, en púrpura y en azul, en lino y en carmesí; asimismo sabe esculpir toda clase de figuras, y sacar toda forma de diseño que se le pida, con tus hombres peritos, y con los de mi señor David tu padre.” (2 Crónicas 2:11-14)
Tremenda recomendación y mas viniendo del Rey de Tiro, que eran una potencia comercial en aquella época!
Pero esto también nos enseña que no podemos interpretar la Biblia con nuestra mente occidental, ya que fue escrita en otra época y en otra cultura. Si no hacemos caso a esta advertencia, erraremos, y después nos acusarán de querer hacerle decir a la Biblia lo que la biblia no dice o no fue la intención del autor decir.
Lamentablemente, todos los hiper racionalistas criticones que tratan de negar la inerrancia de la Biblia, ni siquiera se acercan a ella con intenciones de hallar la verdad, sino mas bien con el único motivo de probar que es inexacta, errante, indigna de confianza, llena de errores, y mas aún.
«La novela Contacto de Carl Sagan —sobre la que luego se filmó la película homónima— toma a π (aunque no en base decimal) como un número que esconde la esencia misma del universo.»[18] Quizás tomar a Pi=3, sin decimales, puede significar un simbolismo de la trinidad, no digo que sea, pero es posible, ya que como expliqué antes este mar de bronce tenía un simbolismo, al ser consagrado a Dios: “Este enorme mar parece simbolizar el gran mar cósmico, que era para los antiguos la fuente de la vida y la fecundidad”»[19]
Ver ¿Es válida la teomática (el uso de los números para verificar la Biblia) como defensa de las Escrituras?
Lamentablemente, uno no tiene respuestas para los porqués de los seres humanos ni respuesta para todos los problemas matemáticos que surgen.

Paul Halmos
Para los porques de los seres humanos, solo tengo por respuesta sincera y verdadera que el único que conoce los corazones y escudriña las mentes es Dios y para los problemas matemáticos la respuesta que mas me gusta es la de una cita de Paul Halmos, matemático estadounidense nacido en Hungría en 1916, quien dijo una vez que “El corazón de las matemáticas son sus propios problemas“.[20]
Lo que me queda bien claro de esta investigación, es que la biblia de ningún modo ni en este pasaje ni en otro, está haciendo hincapié en un modelo matemático en desmedro de otro, y mucho menos en este relato, que lo mas importante es la construcción del templo del rey Salomón, por parte de un especialista altamente capacitado, recomendado por el rey de Tiro especialmente para el rey Salomón.Esa es la trama del contexto de este relato. De ahí en mas, solo leyendas de origen masónico que hablan de Hiram y sus posibles amores con la Reina de Saba, que culminaron en su supuesta muerte (ver Hiram Abiff)
También hay otras leyendas sobre El asesinato de Hiram Abif (ver HIRAM ABiF Leyenda o Realidad?), pero como explico, son TODAS LEYENDAS.
Hay que tener en cuenta que en el papiro egipcio Rhind, datado alrededor de 1650 a.C., ya se daba el valor de 3,16 para el número pi.[21]
Donald Page, físico católico de la Universidad de Alberta en Canadá, autor de trabajos conocidos en coautoría con el mítico Stephen Hawking.
Sobre los ataques a la Biblia por pi=3, Page puntualiza que el cociente entre el perímetro y el diámetro de un círculo es 3.1415… sólo cuando el círculo está dibujado en un plano. Pero en una superficie curva (o en un espacio curvo) la cosa no es así: para ir de un punto de un círculo trazado en la Tierra (un paralelo digamos) a su centro (el polo norte) el camino más directo (el radio) es por un meridiano, y se recorre una distancia mayor al radio del mismo círculo en un plano. ¿Se refiere la Biblia a un mar en un espacio curvo? Dudoso, pero “matemáticamente” posible.[22]
Pero yo averigue sobre esto si era posible y me respondió un científico español, el dr. M.Hernandez, especialista en zoología , que “el único problema es que para que el radio del “circulo curvo” se desviara significativamente de 3,1415… (aunque solo fuera unas décimas), debería ser varios órdenes de magnitud mayor que 30 codos de perímetro. En un círculo de ese tamaño, la curvatura del planeta es despreciable y ni loco llega a 3,0.”[23]
También un cristiano comentó en un debaate que surgió en un blog que “Sobre pi y otros asuntos: La Biblia es un libro de cronología e instrucciones, no un tratado de ingeniería. El que escribió fue un simple cronista, porque lo importante fue el relato de lo que se hizo, no cómo se hizo.” [24]
Una última cosa que debemos también comprender que se deduce de la lectura de la Biblia, y es que Israel estaba rodeado de países que estaban mas desarrollados en sus conocimientos científicos que Israel, Egipto y Babilonia tenían mas desarrollo del conocimiento que Israel. Israel solo superaba al resto de las naciones en su moral.
Esto ya se vislumbra desde los tiempos de Abraham. Pablo Hoff comenta al respecto “ Tanto el mundo antediluviano como el de la Torre de Babel ponen en relieve que no obstante el progreso material y el nacimiento de las civilizaciones, el hombre fracasaba moral y espiritualmente.”[25]
Artículos relacionados
Recomiendo http://tematicacristiana.blogspot.com/2010/04/dice-la-biblia-que-pi-3.html ,ya que esta actualizado
http://lasteologias.wordpress.com/2010/03/08/el-valor-de-pi-revelado-en-la-biblia/
Notas:
[0] Pablo Hoff, Los libros Históricos, Pág. 161, edit. vida, undécima impresión, 1993,EE.UU.
[1] Nuevo Diccionario Bíblico 1a. edición (basada en la segunda edición inglesa del New Bible Dictionary, 1982) , pág. 1333,Edit. Certeza
[2] http://es.wikipedia.org/wiki/N%C3%BAmero_real
[3] http://es.wikipedia.org/wiki/N%C3%BAmero_%CF%80
[4] <!--[endif]--> http://www.antesdelfin.com/foro/showthread.php?t=11099
[5] http://mensajeros.blog.com/2918097/
[6] Los libros Históricos, op. cit. pag. 161
[7] Nota al pie de página:1 Reyes 7:26 RV 1995
Nota:
También podes bajar una biblia electrónica gratis de internet y encontrar el artículo en esa biblia electrónica, en la traducción 1995 de reina Valera ( e-Sword® Version 7.8.5 Copyright © 2000-2007 Rick Meyers , 5902 Parham Road Franklin, TN 37064 United States of America www .e -sword .net )
[8] http://foros.monografias.com/showthread.php?t=33021&page=2&pp=10
[9] http://www.sindioses.org/humor/criticas.html
[10] http://www.dormilones.net/2007/06/13/pi-3-lo-pone-en-la-biblia/
[11] Nelson, Wilton M., (Hiram).Nuevo Diccionario Ilustrado de la Biblia, (Nashville, TN: Editorial Caribe) 2000, c1998.
[12] <!--[if gte mso 9]> Normal 0 21 false false false MicrosoftInternetExplorer4 <![endif]--><!--[if gte mso 9]> <![endif]--> <!--[endif]-->Nelson, Wilton M., (Hiram).Nuevo Diccionario Ilustrado de la Biblia, (Nashville, TN: Editorial Caribe) 2000, c1998.
[13] http://senosva.blogia.com/2007/102901-y-jesus-llegara….php
[14] http://it.answers.yahoo.com/question/index?qid=20080425060745AAElDZP (comentario de chess fan)
[15] http://humor.orange.es/delocos/curiosidades/ver_curiosidad.php?curiosidad=923
[16] http://www.xtec.es/~bfiguera/curioso6.html
[17] http://tematicacristiana.blogspot.com/2008/06/paul-halmos.html
[18] http://es.wikiquote.org/wiki/Matem%C3%A1tica
[19] Nota al pie de página:1 Reyes 7:26 RV 1995
[20] http://tematicacristiana.blogspot.com/2008/06/paul-halmos.html
[21] http://jolimu.wordpress.com/2008/03/24/eslabones-perdidos-juegan-al-escondido/#comment-598
[22] Física en la Biblia, Alberto Rojo – Diario Critica,http://www.nforo.net/showthread.php?p=441641
[23] http://oldearth.wordpress.com/2008/07/12/%C2%BFquien-insulta-a-quien/#comment-1826
[24] http://oldearth.wordpress.com/2008/07/12/%C2%BFquien-insulta-a-quien/#comment-1831
[25] Pablo Hoff, Pentateuco, pp.49,edit. Vida
“La Geometría existía antes de la Creación. Es co-eterna con la mente de Dios… La Geometría ofreció a Dios un modelo para la Creación… La Geometría es Dios mismo.” Johannes Kepler
Visualización de la definición de π. Es el perímetro de una circunferencia de diámetro 1.
Pasajes bíblicos: A menos que se indique lo contrario, pertenecen a la traducción Reina Valera 1960
Ver I Reyes cap. 7
Ver 2 Crónicas cap. 4
Introducción
La pregunta si la biblia dice que Pi=3, no es difícil de responder. Al principo me pareció que no lo iba a entender, pero a medida que fui investigando, fui hallando mas información de la que yo me imaginaba,
El interés de este artículo es el fuerte ataque de los ateos que pretenden con esto probar que la Biblia está equivocada y derribar la doctrina de la inspiración divina y la inerrancia de las escrituras. Dos doctrinas sumamente importantes a la hora de realizar exégesis bíblica o de una correcta apologética del cristianismo.
Vemos que podemos deducir del estudio de este pasaje bíblico para hallar una óptima respuesta. Este pasaje (I Reyes cap. 7:23), está en el contexto de la narración de la construcción del templo de Salomón. Un hermoso templo que este rey construyó, en un periodo de 13 años. Ya su padre, el rey David había querido hacerlo, pero el Señor no se lo permitió, pues había derramado demasiada sangre de sus enemigos. Por lo tanto, solo pudo comprar el terreno, y destinar los recursos para que su hijo Salomón inicie la construcción.

Representación del Templo de Jerusalén reconstruido por Herodes
Pablo Hoff comenta que «El templo de Salomón se asemejaba algo a los templos paganos, pero con algunas diferencias importantes. En el templo salomónico, no se encontraba asomo alguno de idolatría. En el lugar santísimo no había imagen ni representación alguna de Dios, pues Dios es espíritu y no se le puede representar materialmente. »[0]
El diccionario bíblico explica que «en la Mesopotamia, de donde salió Abraham, cada ciudad tenía un templo dedicado a su deidad patronal. Se consideraba que ese dios era el propietario de la tierra, y si no recibía su bendición esa tierra habría de resultar improductiva, lo cual daría como resultado ingresos pobres para su templo. El rey o gobernante local actuaba como mayordomo del dios. No tenía sentido que los patriarcas seminómades edificasen un santuario fijo para su Dios. Él se les revelaba en los lugares y en la forma que a él le placía. A veces esas ocasiones ofrecían motivo para la erección de un altar para sacrificios. A veces se conmemoraba dicho acontecimiento con una columna (Gn. 28.22, VRV2 “piedra”).
Una vez que Israel adquirió características de nación se hizo necesario contar con un santuario central, un lugar de reunión para todo el pueblo, símbolo de su unidad en el culto a su Dios. Esta necesidad la suplió primero el tabernáculo durante la peregrinación por el desierto, y luego los santuarios reconocidos durante el periodo de los jueces (p. cj. Siquem, Jos. 8.30ss; 24.1ss; Silo, 1 S. 1.3).
Las naciones de Canaán tenían sus propios templos, llamados simplemente “casa de Dagón” o casa de la deidad que fuera patrona de la ciudad correspondiente (hcb. bét Aagon, 1 S. 5.5; bét ‘astarót, 1 S. 31.10; cf. bét yhwh, Ex. 23.19). Se han encontrado varios de estos templos en Bet-sán, Hazor, y otros sitios.
Tintoretto: «La reina de Saba y Salomón» (ca. 1555). Museo del Prado
La falta de un santuario dedicado a Yahvéh aparecía como una afrenta cuando David hubo consolidado su posición y edificó un palacio permanente para sí mismo. Dijo entonces el rey *yo habito en casa de cedro, y el arca de Dios está entre cortinas” (2 S. 7.2). No le fue dado el que edificase el templo, porque sus propias manos estaban teñidas de la sangre de sus enemigos, pero él reunió los materiales, reunió fondos, y adquirió un lugar adecuado (1 Cr. 22.8, 3; 2 S. 24.18-25). Salomón inició la construcción en el año cuarto, y el templo se completó siete años después (I Re. 6.37-38).
El templo de Salomón, el que se encontraba en la zona llamada ahora “Haram esh-Sherif” en el lado oriental de la “ciudad antigua” de Jerusalén es algo que no se discute. La ubicación precisa dentro del vasto recinto resulta más incierta. La parte más alta de la roca (ahora cubierta por el edificio conocido como “La cúpula de la roca”) puede haber sido el lugar del santuario de mas adentro o del altar de los holocaustos. en la parte exterior (2 Cr. 3:1). Presumiblemente esta roca constituía parte de la era de Arauna,comprada por David por uina suma que se indicaba en cincuenta ciclos de Plata ( 2 Sam. 24:24) o 600 ciclos de oro (I Cro. 21:25)
De la estructura de Salomón no queda nada en pie, y durante las excavaciones auspiciadas por el Fondo para la Exploración de la Palestina no se encontraron rastros concretos de la misma. Más aun, es probable que la tarea de nivelar la roca y de edificar los grandes muros de apoyo para el atrio del templo de Herodes hayan borrado todo vestigio de construcciones anteriores.
Los pasajes de 1 R. 6-7 y 2 Cr. 3-4 deben servir de base para cualquier reconstrucción del templo de Salomón. Dichos relatos, si bien detallados, no abarcan todos los aspectos, no se entienden perfectamente, y contienen algunas aparentes discrepancias (p. ej. 1 R. 6.2 y I6s). Pueden ser complementadas con referencias incidentales, y por la descripción del templo de Ezequiel, versión ampliada del edificio de Salomón (Ez. 40-43). El templo propiamente dicho era rectangular, orientado de E a O. Es razonable suponer que, como el templo de Ezequiel, se encontraba sobre una plataforma (cf. Ez. 41.Ocho). No se dan las dimensiones de la zona circundante. Siguiendo nuevamente el plano de Ezequiel, parecería que hubo dos patios, interior y exterior; sugerencia apoyada por 1 R. 6.36; 7.12; 2 R. 23.12; 2 Cr. 4.9.
Maqueta del Templo
EL REY SALOMÓN Y SU TEMPLO
El altar de bronce para los sacrificios se encontraba en el patio interior (1 R. 8.22,64; 9.25). Tenía 20 codos de lado, y 10 codos de altura (2 Cr. 4.1). Entre este y el pórtico se encontraba la fuente de bronce que contenía el agua para las purificaciones rituales (el “mar … fundido”, 1 R. 7.23-26). Este gran receptáculo, de 10 codos de diámetro, descansaba sobre cuatro grupos de cuatro bueyes de bronce orientados hacia los cuatro puntos cardinales. Fueron retirados por Acaz (2 R. 16.17).
En la dedicación del templo Salomón se ubicó sobre un “estrado” (2 Cr. 6.12s, heb. kiyyor, palabra que se usa para “fuente” en otras partes, Ex. 30.18, etc.; aquí puede significar fuente invertida), lo cual tiene paralelos en las esculturas sirias y egipcias, y posiblemente en las acádicas (véase W. F. Albnght, Archaeology and the Religión of lsraeL, 1953, pp. 152-154).
Una serie de escalones probablemente llevaba del patio interior al pórtico (heb. ‘úlam). La entrada tenía dos columnas, Jaquín y Boaz, con capiteles profusamente ornamentados. Su función es incierta; no constituían parte de la estructura. Es probable que hubiera puertas para cerrar el pasillo (cf. Ez. 40.48).
El pórtico medía 10 codos de largo y 20 codos de ancho (sobre la longitud del codo, véase pesos y medidas). Su altura se indica como 120 codos (2 Cr. 3.4), pero seguramente se trata de un error, porque el resto del edificio sólo tenía 30 codos de altura. Al O del pórtico se encontraba la gran cámara en la que se llevaban a cabo las ceremonias rituales ordinarias. Este “lugar santo” (heb. hékal, palabra derivada, a través del cananeo, del sumerio E. GAL, ‘casa grande’) medía 40 codos de longitud, 20 de anchura, y 30 de altura. Puertas dobles de madera de ciprés lo separaban del pórtico, y cada puerta se componía de dos hojas.”»[1]
El Templo de Jerusalén tal como lo imaginó un teólogo alemán del siglo XVI. Las seis torres, el frontón triangular clásico, las dos columnas exentas coronadas con esferas tienen su contrapartida en esta imagen de como pudo ser El Escorial en las primeras fases del proyecto
II.Comentarios sobre Matemáticas
Haremos un breve repaso histórico de Matemáticas. El número pi es número matemático, de tipo real, ya que contiene decimales. Su importancia de conocer de la historia de este número es ver si el autor del mar de bronce, construido en el interior del templo, conocería o no los números reales, ya que como vemos, se utilizó un valor exacto (Pi=3) y se obviaron los decimales.
a.¿Quien descubrió los números reales?
«Los egipcios utilizaron por primera vez las fracciones comunes alrededor del año 1000 a. C.; alrededor del 500 a. C. el grupo de matemáticos griegos liderados por Pitágoras se dio cuenta de la necesidad de los números irracionales. Los números negativos fueron inventados por matemáticos indios cerca del 600, posiblemente reinventados en China poco después, y no se utilizaron en Europa hasta el siglo XVII, si bien a finales del XVIII Leonhard Euler descartó soluciones negativas para las ecuaciones porque lo consideraba irreal. En ese siglo, en el cálculo se utilizaba un conjunto de números reales sin una definición concisa, cosa que finalmente sucedió con la definición rigurosa hecha por Georg Cantor en 1871.
En realidad, el estudio riguroso de la construcción total de los números reales exige tener amplios antecedentes de teoría de conjuntos y lógica matemática. Fue lograda la construcción y sistematización de los números reales en el siglo XIX por dos grandes matemáticos europeos utilizando vías distintas: la teoría de conjuntos de Georg Cantor (encajamientos sucesivos, cardinales finitos e infinitos), por un lado, y el análisis matemático de Richard Dedekind (vecindades, entornos y cortaduras de Dedekind). Ambos matemáticos lograron la sistematización de los números reales en la historia no de manera espontánea, sino echando mano de todos los avances previos en la materia: desde la antigua Grecia y pasando por matemáticos como Descartes, Newton, Leibniz, Euler, Lagrange, Gauss, Riemann, Cauchy y Weierstrass, por mencionar sólo a los más sobresalientes.»[2]
b. Historia de Pi [3]

b.0. Referencias bíblicas a Pi
Una de las referencias documentadas más antiguas al número pi se puede encontrar en un versículo poco conocido de la Biblia
I Re. 7:23:RV 1960 “Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos.”
Se puede ver cómo una idea similar se puede encontrar en II Crónicas 4:2.
“También hizo un mar de fundición, el cual tenía diez codos de un borde al otro, enteramente redondo; su altura era de cinco codos, y un cordón de treinta codos de largo lo ceñía alrededor.”
En él aparece en una lista de requerimientos para la construcción del Gran Templo de Salomón, construido sobre el 950 a. C. y su interés aquí radica en que da un valor de π = 3,0.
b.1.Época egipcia
El uso del número π en las culturas antiguas se remonta al que hacía el escriba egipcio Ahmes en el año 1800 a. C., descrito en el papiro de Rhind, donde se emplea un valor de π afirmando que el área de un círculo es similar a la de un cuadrado cuyo lado es igual al diámetro del círculo disminuido en 1/9, es decir igual a los 8/9 del diámetro. Es decir que:

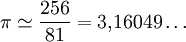
Entre los ocho documentos matemáticos de la cultura egipcia hallados hasta hoy, en sólo dos se habla de círculos. Uno es el papiro de Rhind y el otro es el papiro de Moscú. Sólo en el primero se habla del cálculo del número π. El investigador Otto Neugebauer, en un anexo de su libro «The Exact Sciences in Antiquity», describe un método supuestamente inspirado por los problemas del papiro de Ahmes para averiguar el valor aproximado de π mediante aproximación a un cuadrado de lado 8/9 del diámetro.
Algunos matemáticos mesopotámicos empleaban en el cálculo de segmentos valores de π iguales a 3, alcanzando en algunos casos valores más refinados de 3 y 1/8.
b.2.Época griega

Método de Arquímedes para encontrar dos cotas que se aproximen al número π.
El matemático griego Arquímedes (siglo III a. C.) fue capaz de determinar el número π entre el intervalo comprendido por 3 10/71, como valor mínimo y 3 1/7, como valor máximo. Con esta aproximación de Arquímedes se obtiene un valor con un error que oscila entre 0,024% y 0,040% sobre el valor real. El método empleado por Arquímedes era muy simple y consistía en circunscribir e inscribir polígonos regulares de n-lados en circunferencias y calcular el perímetro de dichos polígonos. Arquímedes empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.
En el siglo II, Claudio Ptolomeo proporciona un valor fraccionario por aproximaciones:

b.3.La matemática persa y china
El cálculo de pi fue una atracción para todas las culturas con matemáticos dedicados, de esta forma se tiene que el matemático chino Liu Hui fue el primero en sugerir que 3,14 era una buena aproximación, usando un polígono de 96 lados. Posteriormente estimó π como 3,14159 empleando un polígono de 3072 lados.
En el siglo V, el matemático y astrónomo chino Zu Chongzhi calculó π en 3,1415926 al que llamo «valor por defecto» y 3,1415927 «valor por exceso», y dio dos aproximaciones racionales de π: 22/7 y 355/113 muy conocidas ambas, siendo la ultima aproximación tan buena y precisa que no fue igualada hasta 900 años después, en el siglo XV
En el siglo XV, el matemático persa Ghiyath al-Kashi fue capaz de calcular π con 9 dígitos empleando una base numérica sexagesimal, lo que equivale a una aproximación de 16 dígitos decimales: 2π = 6,2831853071795865.
b.4.Renacimiento europeo


John Wallis, (1616–1703)

Leonhard Euler, (1707–1783)
A partir del siglo XII, con el uso de cifras arábigas en los cálculos, se facilitó mucho la posibilidad de obtener mejores cálculos para π. El matemático Leonardo Pisano, en su «Practica Geometriae», amplifica el método de Arquímedes, proporcionando un intervalo más estrecho. Algunos matemáticos del siglo XVII, como Vieta, usaron polígonos de hasta 393.216 lados para aproximarse con buena precisión a 3,141592653.
El matemático inglés John Wallis desarrolló en 1655 la conocida serie Producto de Wallis:
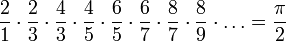
De la misma forma Leibniz calculó de una forma más complicada en 1682 la siguiente serie que lleva su nombre:
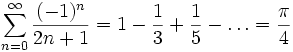
b.5.Época moderna (pre-computacional)
Fue en el año 1706 cuando el galés William Jones afirmó «3,14159 andc. = π». Leonhard Euler adoptó el conocido símbolo en 1737 e instantáneamente se convirtió en una notación estándar hasta hoy en día.
En 1610 el matemático Ludolph van Ceulen calculó los 35 primeros decimales de π. Se dice que estaba tan orgulloso de esta hazaña que lo mandó grabar en su lápida. Los libros de matemática alemanes durante muchos años denominaron a π como número ludofiano.
El matemático japonés Takebe empezó a calcular el número π en el año 1722 con el mismo método expuesto por Arquímedes, y fue ampliando el número de lados para polígonos circunscritos e inscritos hasta llegar a 1.024 lados. Este ingente trabajo consiguió que se determinara π con 41 decimales.
Johan Heinrich Lambert(1728-1777), matemático alemán, probó que Pi es irracional. (Un número irracional no se puede escribir en forma de fracción racional. Números racionales son : 1, 2 , 3/4, 17/23)» [4]
En 1789 el matemático de origen eslovaco Jurij Vega, mediante la fórmula de John Machin descubierta en 1706, fue el primero en averiguar los primeros 140 decimales de π, de los cuales 126 eran correctos; este récord se mantuvo durante 52 años, hasta que en 1841 William Rutherford calculó 208 decimales de los cuales 152 eran correctos.
El matemático aficionado de origen inglés William Shanks consumió cerca de 20 años de su vida calculando π con 707 decimales (evento acaecido en 1873). En el año 1944, D. F. Ferguson encontró un error en la posición decimal 528, a partir del cual todos los dígitos posteriores eran erróneos. En 1947, Ferguson recalculó π con 808 decimales con la ayuda de una calculadora mecánica.
b.6.Época moderna (computacional)

Desde el diseño de la primera computadora se empezaron a desarrollar programas para el cálculo del número π con la mayor cantidad de cifras posibles. De esta forma, en 1949 un ENIAC fue capaz de romper todos los récords del momento con 2037 lugares decimales (en 70 horas). Poco a poco se fueron sucediendo los ordenadores que batían récords, y de esta forma pocos años después (1954) un NORAC llegó a 3092 cifras. Durante casi toda la década de los años 1960 los IBM fueron batiendo récords, hasta que un IBM 7030 pudo llegar en 1966 a 250.000 cifras decimales (8 h y 23 min). Durante esta época se probaban las nuevas computadoras con algoritmos para la generación de series de números procedentes de π.
Ya en la década de 2000, los ordenadores eran capaces de sacar cifras récord inmensamente grandes; en 2004 fueron capaces de sacar 1,3511 billones de lugares decimales mediante el uso de una supercomputadora Hitachi, que llegó a trabajar sólo 500 horas para realizar el cálculo.
Año 1949 Descubridor Ordenador utilizado Número de cifras decimales
G.W. Reitwiesner y otros
ENIAC
2.037
1954
NORAC
3.092
1959
Guilloud
IBM 704
16.167
1967
CDC 6600
500.000
1973
Guillord y Bouyer
CDC 7600
1.001.250
1981
Miyoshi y Kanada
FACOM M-200
2.000.036
1982
Guilloud
2.000.050
1986
Bailey
CRAY-2
29.360.111
1986
Kanada y Tamura
HITAC S-810/20
67.108.839
1987
Kanada, Tamura, Kobo y otros
NEC SX-2
134.217.700
1988
Kanada y Tamura
Hitachi S-820
201.326.000
1989
Hermanos Chudnovsky
CRAY-2 y IBM-3090/VF
480.000.000
1989
Hermanos Chudnovsky
IBM 3090
1.011.196.691
1991
Hermanos Chudnovsky
2.260.000.000
1994
Hermanos Chudnovsky
4.044.000.000
1995
Kanada y Takahashi
HITAC S-3800/480
6.442.450.000
1997
Kanada y Takahashi
Hitachi SR2201
51.539.600.000
1999
Kanada y Takahashi
Hitachi SR8000
68.719.470.000
1999
Kanada y Takahashi
Hitachi SR8000
206.158.430.000
2002
Kanada y otros
Hitachi SR8000/MP
1.241.100.000.000
2004
Hitachi
1.351.100.000.000

En la época computacional del cálculo de π las cifras se han disparado, no sólo debido a la potencia de cálculo que estas máquinas son capaces de generar, sino también por el prestigio que conlleva para el constructor de la máquina el que su marca aparezca en la lista de los récords.
II. Construcción del Templo del rey Salomón
«El Rey Salomón acababa de terminar el Templo cuando se dispuso a construir un palacio para él y su corte. Tardó trece años en construirlo, y la Biblia cuenta con bastante lujo de detalles cómo llevó acabo su proyecto. Los pórticos, las columnas, los capiteles, las fuentes… pero hay un elemento en particular que es de interés matemático.

Letra griega pi. Símbolo adoptado inicialmente en 1706 por William Jones y popularizado por Euler.
Ver Temas relacionados con Pi
HISTORIA DEL NÚMERO PI
Algunas curiosidades sobre el número Pi (pi)
Dice así el texto sagrado:
I Reyes 7:23
RV 1960 “Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos.”
RV 1909 “Hizo asimismo un mar de fundición, de diez codos del un lado al otro, perfectamente redondo: su altura era de cinco codos, y ceñíalo alrededor un cordón de treinta codos.”
NVI “Hizo también una fuente circular de metal fundido, que medía cuatro metros y medio de diámetro y dos metros con veinticinco centímetros de alto. Su circunferencia, medida a cordel, era de trece metros y medio.”
RV 1995 “Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo. Tenía cinco codos de altura y a su alrededor un cordón de treinta codos.”
LBLA “Hizo asimismo el mar de metal fundido de diez codos de borde a borde, en forma circular; su altura era de cinco codos, y tenía treinta codos de circunferencia.”
Reina-Valera Antigua “Hizo asimismo un mar de fundición, de diez codos del un lado al otro, perfectamente redondo: su altura era de cinco codos, y ceñíalo alrededor un cordón de treinta codos.”
Este “mar” al que se está refiriendo el texto es un monumental cuenco de bronce parecido al que vemos en la imagen. La altura, 5 codos, es el único dato que no nos interesa. Lo demás sí:
1. Es “perfectamente redondo” (una circunferencia).
2. Tiene “diez codos de un lado al otro” (diámetro = 10 codos)
3. “Lo ceñía un cordón de treinta codos” (longitud de la circunferencia = 30 codos)
Recordemos que el número pi se obtiene de dividir la longitud de la circunferencia entre el diámetro. En este caso pi = 30/10 = 3. Sin decimales, 3 es una aproximación bastante burda si la comparamos con la retahíla de 3,141592… que todos conocemos de la primaria. Pero para el tiempo de Salomón (sobre el 950 a.C), y en sintonía con su aclamada sabiduría, era una medición exquisita.
Sin embargo no era la primera medición expresa del misterioso número. Los Egipcios dieron con un valor de 25/8 = 3,125. No está nada mal. Los Mesopotámicos asemejaron pi al valor de la raíz cuadrada de 10, que es 3,162. La historia de cómo llegaron a esta comparación sobrepasa el presente artículo, pero es bien interesante.
Escultura de Pi en la ciudad de Seattle
En defensa de los peritos de Salomón cabe decir que la “perfecta redondez” de semejante chisme probablemente no era tan fácil de conseguir. También hay quien defiende que el cuenco tenía un borde grueso de forma que el diámetro se midió para el borde interior, mientras que la longitud de la circunferencia se midió para el borde exterior, dando el dando el error de pi que observamos.
En cualquier caso fue el comienzo de una serie de aproximaciones a pi seguidas por la primera aproximación teórica (de Arquímedes), luego Ptolomeo, el chino Zu Chongzhi, los árabes al-Khwarizmi y al-Kashi, y seguida finalmente por numerosos europeos del Renacimiento y la Ilustración que consiguieron aproximadamente los primeros 500 dígitos de pi.

Hoy en día los ordenadores se han convertido en herramienta fundamental para el cálculo de pi. Se han calculado con éxito un total de 51000 millones de decimales. Sin embargo el afamado número sigue sin querer contarnos todos sus secretos, a la vez que nos plantea nuevas incógnitas.
Cada 14 de Marzo (3/14 según el calendario sajón) se celebra el día de pi. Para los más frikis (neologismo que galopante se abre paso entre nosotros, y que denota a los fanáticos de aficiones no destructivas pero sí extravagantes) no sólo se celebra el día, sino el momento de pi: El 14 de Marzo a la 1 de la mañana, 59 minutos y 26 segundos, que todo junto nos da 3,1415926.
Rarezas aparte, estamos ante un estudio de milenios de edad que todavía sigue sorprendiéndonos, y que hemos conseguido relacionar con muchas disciplinas. Peter Borwein lo resume de forma magistral: “Hay una belleza en pi que nos hace seguir mirándolo… Los dígitos de pi son extremadamente aleatorios. No tienen ningún patrón, y en matemáticas eso es lo mismo que decir que tiene todos los patrones”. Por eso precisamente es tan fascinante.»[5]
En 1 Reyes 7:23, hablando del Templo de Salomón dice:
”Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos.”
Pablo Hoff comenta que «La obra de arte del mar de fundición,(el pilón de agua lustral,ubicado en el atrio),era meramente de adorno»[6]
Pero aparentemente tenía un simbolismo:
«Este enorme mar parece simbolizar el gran mar cósmico, que era para los antiguos la fuente de la vida y la fecundidad. Su uso estaba reservado exclusivamente a los sacerdotes, para diversos tipos de purificaciones. En 2 R 16.17; 25.13 se habla del fin que tuvo esta bella obra de arte.»[7]
Ver Pesos y medidas usados en la biblia
¿Está equivocada la Biblia?
«…el mar de bronce del que habla, es, en realidad, un cilindro, con altura de cinco codos, que a nuestros efectos es irrelevante, pero el diámetro es de diez codos, por tanto, si la circunferencia es de 30 codos, tenemos que el valor de pi vale 3.
Además, es imposible lo que dice, pues el valor de la circunferencia sería 31,4 codos, por lo que un cordón de 30 codos nunca podría ceñir el cilindro, se quedaría corto. Debería ser, al menos, 32 codos.
No creo que haya que saber muchas matemáticas, en general una sencilla aproximación basta siempre para las cosas diarias.
El problema es que el valor de pi era conocido 700 años antes en Babilonia y en Egipto, por lo que, siendo la biblia un libro inspirado por Dios debe, al menos, reflejar los conocimientos de la época. Reflejar menos implica que eran unos ignorantes los redactores, lo cual no se lleva muy bien con la inspiración divina.
Un cordón de 30 codos (o lo que sea) no puede ceñir un cilindro de 10 codos de diámetro, es sencillamente imposible…
El cordón medía 30 codos porque ceñía al mar semiesférico bastante por debajo del borde.
Recuerda que el mar fundido en realidad era como una especie de media naranja (perfectamente redondo, según 1 Reyes 7: 23), con el borde formando algo así como una flor de lirio, un detalle decorativo, luego venían por debajo 2 hileras de calabazas. Muy probablemente la soga o cordón bordeaba por debajo de las calabazas, pero es un detalle menor, ya que no necesariamente.¿Entiendes? Nadie está negando que el valor de Pi sea el que es y que tan bien conocían los babilonios y egipcios, y seguramente también los hebreos por el contacto cultural con estas civilizaciones.
El asunto es la ubicación de la soga, que no habría estado en la línea media, sino unos centímetros más abajo, OK?
Fíjate en el esquema que te envío, analízalo bien. Exageré quizás el emplazamiento de la soga para que se entienda mejor lo que te comenté.
La verdad es que con las traducciones, supongo que se pierde el sentido original, no obstante, si fuese esta la solución carece de sentido dar las medidas del cordón que ciñe, ¿por qué no 20 o 25?, pues depende de donde se coloque.
Lo lógico es dar una medida con significado, y la única es la del borde exterior.
A mi me sigue pareciendo más lógica la explicación de que refleja los conocimientos de la época, y los redactores, hebreos de la edad del bronce, tenían unos conocimientos limitados, por supuesto inferiores a Babilonia o Egipto. En general, en los libros de historia de las matemáticas se adopta este criterio, y se mantiene que la aproximación de la Biblia al valor de pi es 3.
En cualquier caso la explicación, al menos, parece plausible.

Si consideramos el dibujo propuesto como una semiesfera tenemos que el Volumen se calcula con
V=2/3 * pi * R3 (R3 = Radio al cubo)
Considerando el codo de 45cm o 0.45m
El Radio es de 5 codos, o sea 2.25m
V=2/3*3.14*2.25*2.25*2.25=23.844 metros cubicos o sea 23844 litros
Tomando el bato de 22 litros (el mas chico que encontre ya que varia hasta 37 litros)
22384/22=1084 batos
Ahora considerándolo cilíndrico (lo que descarta el dibujo propuesto) el tenemos V=pi*R2*h (R2=radio al cuadrado)
La altura es de 5 codos, o sea 2.25 m
V=3.14*2.25*2.25*2.25=35.766 metros cúbicos o sea 35766 litros
En batos=1625
Esto es considerando el borde externo y que esta lleno hasta el tope
Por lo tanto no entran los 2000 batos indicados en Reyes y menos los 3000 indicados en 2 Crónicas.
Quizás las medidas de los codos y los batos están mal….. Quizás
A ver. Saquemos los cálculos del medio.
Reyes 7:23 Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos.
Pi es la relación entre la longitud de la circunferencia y su diámetro. En este caso el cordón que mide 30 codos /10 codos = 3 y no 3,14159….. Esto significa que el cordón no alcanza a rodear el recipiente.
La solución posteada por Migdol es la de un recipiente con forma de una semiesfera (como una pelota partida al medio) y colocar el cinturón por debajo del borde superior a una altura donde la circunferencia mida 30 codos y hacer aparecer el número pi.
El problema de esta solución es que esta forma disminuye considerablemente la capacidad del recipiente y según Reyes 7:26 …y cabían en él dos mil batos. (aprox 44000 litros)
El recipiente semiesférico solo puede contener 24000 litros
Otra solución podría ser la del dibujo donde el borde superior tiene los 10 codos de diámetro pero el problema sigue siendo el volumen del recipiente, en este caso 36000 litros.
El otro tema es que en 2 Crónicas 4:5 dice … Y le cabían tres mil batos (aprox 66000 litros)
O sea que a pi lo podemos hacer aparecer ya que la descripción es muy imprecisa. Lo que no podemos es almacenar la cantidad de liquido indicada.
El valor de pi=3 no está tan mal para la época. Lo babilonios por aquel entonces pensaban que pi era tres. Pero los egipcios unos siglos antes ya habían ido más lejos al expresar a pi como (4/3)^4=3,16. Pero es estéril la discusión con cualquier fanático. te pondrá la cuerda dónde le interese.» [8]
Críticas a la geometría
En el portal sindioses, encontré un artículo muy gracioso, escrito con muy buen sentido del humor, sobre este tema, de Pi=3 «En la Biblia se afirma que pi vale 3 (1 Reyes 7:23), por lo que debemos enseñarlo así en los cursos de geometría para que sean correctos, ¿por qué cree usted hermano, que los edificios no soportan los terremotos? ¡Porque no los fabrican con el verdadero valor de pi!!!!!. Si los fabricaran con un valor de pi igual a tres, las construcciones ganarían solidez debido a la gracia divina que los protegería de todo mal basados en que el tres ¡es el numero de la Trinidad! Y por la gracia de las Tres Personas los edificios quedarían protegidos contra todo mal. Además, el valor actual de pi es un numero feo, difícil de recordar y ¡aproximado!, si amigo lector, es verdad, ellos no quieren que se sepa pero es verdad, el valor real que ellos consideran de pi es desconocido ¿cómo pueden estos que nos hablan de ciencia decir que sus matemáticas son exactas si ni siquiera conocen el valor de este número? ¿Cómo pueden construir cosas sólidas si no tienen precisión al medir?. En cambio Dios en su infinita sabiduría lo hizo exactamente igual a tres para que no hubieran aproximaciones y pudiera ser exacto y justo todo lo que es circular, amén hermanos que les hablo como me fue revelado y el hecho de que pi valga 3 es una hermosa prueba de que Dios existe y es trino, así lo nieguen los ciegos de mente cerrada que no ven más allá de sus narices y son incapaces de romper sus dogmas. ¡Alabado sea el señor por toda la eternidad! » [9]
En respuesta a esta críticas escrita en un bueno y sano sentido de humor, mas allá de que en el fondo es un crítica, creo que es importante responder este tema mirando a Jesús, quien en su época fue confrontado por una persona muy astuta e inteligente quien le preguntó sobre si estaba bien pagar los impuestos al gobierno de esa época; hoy también muchos preguntan y cuestionan con astucia sobre si la participación cívica, social y política de los cristianos es correcta. O si debemos enseñar ciencia en las aulas o religión a los alumnos.
La respuesta de Jesús (Lucas 20:25) debe ayudarnos a dar la nuestra hoy. Jesús respondió: “Dad a César lo que es de César, y a Dios lo que es de Dios.”
Si leemos bien la respuesta que Jesús dio a esa persona de sus días, nos daremos cuenta que el Maestro no negó la existencia del Estado y sus reglas relacionadas con los impuestos, sino que animó a los oyentes a ser responsables tanto con el Estado como con Dios. Y lo mismo podemos decir con respecto a las enseñanzas de la ciencia. Después de todo, los seguidores de Cristo creemos que Dios es soberano sobre todo y en todos. Si las autoridades del pais en el que nos toca vivir determinan un plan de enseñanza, los cristianos debemos respetarlo, aunque no nos guste o no estemos de acuerdo en lo que respecta a nuestra fe.
Si el gobierno nos prohibiera creer en Cristo, bueno, ahí sí se terminó la obediencia.Pero en este tema, no veo ninguna agresión a la fe cristiana ni ninguna necesidad de afirmar que Pi=3, cuando tampoco la biblia lo enseña.Repito lo que ya he comentado, es tan solo una narración histórica de como fue construido el templo del rey Salomón y no una discusión matemática sobre la superioridad de un valor sobre otro.
Pero si la ciencia hoy en dia ha determinado que Pi=3,1416…, y eso es lo que se enseña en las escuelas, pues hay que estudiar lo que se enseña, ya que esto no afecta nuestra fe cristiana en absoluta.
Además, tampoco el pasaje bíblico en cuestión está realizando una apologética o defensa de la superioridad de un valor matemático sobre otro. Simplemente está narrando los hechos relacionados con la construcción del templo de Salomón.

Pi = 3. ¿Lo pone en la Biblia?
«7:23 Él hizo además el Mar de metal fundido, que medía cinco metros de diámetro y tenía forma circular; su altura era de dos metros y medio, y una cuerda de quince metros medía su circunferencia.
Para aquellos que no recuerdan muy bien como calcular el número Pi, o sea este π, vamos a ponerlo de forma simple.
Bien pues π = 3.141592… ya que si tuviéramos una cuerda alrededor de una circunferencia de diámetro 1, la cuerda tendría una longitud de 3.141592…, para que lo veáis de forma más gráfica.
Bien, pues la proporción de las sagradas escrituras es que el diámetro = 5 por lo que echando unos cálculos simples llegamos a la conclusión de que la cuerda que medía su circunferencia debería ser igual a… 15.70… Pero no, es 15, ni más ni menos, y como esta en las sagradas escrituras pues…
Ah, es verdad, no recuerdo que ningún cristiano radical halla puesto en duda que Pi = a 3.141592, es más, seguramente digan que es un error de traducción o que sea simplemente una historia narrativa representativa y que no se tienen que tomar en cuanta lo números… Entonces por qué se ceban en creer que el creacionismo , porque no lo ven como una historia narrativa representativa del poder divino, y sí como el comienzo de la historia de la humanidad.
Como bien dice el artículo. Si Dios hizo al hombre porque lo pone en la Biblia, π = 3 por la misma razón. Es lo que tiene creer en algo tan fuera de lugar, que o todo o nada.»[10]
Ver La Biblia (I)
HIRAM
Hiram ensena los planos a Salomon.
Grabado de J.J. Scheuchzer
"Physica Sacra Iconibus Illustrata"
Ausburgo, 1731
Nombre del «artífice a quien el rey de TIRO, del mismo nombre, envió a Salomón para que hiciese las decoraciones en bronce del templo (1 R 7.13–47; 2 Cr 2.13, 14; 4.11–18). Era hijo de un artífice de Tiro y de una mujer israelita, quizás de la tribu de Neftalí (1 R 7.14) o de la de Dan (2 Cr 2.14). Su principal obra en el templo fueron las dos grandes columnas que recibieron los nombres de Jaquín y Boaz.»[11]
I Reyes 7:23 ” hijo de una viuda de la tribu de Neftalí. Su padre, que trabajaba en bronce, era de Tiro; e Hiram era lleno de sabiduría, inteligencia y ciencia en toda obra de bronce. Este, pues, vino al rey Salomón, e hizo toda su obra.”
Hiram era un experto en el tema de trabajar en bronce. Además, su padre estaba en el mismo oficio, lo que nos muestra que seguramente fue su padre quien el enseño el oficio. No era un ignorante en e oficio del bronce construcción. Su madre era una mujer israelita, seguramente una mujer piadosa.
«Este técnico, fue recomendado por el rey de TIRO, del mismo nombre, Hiram, quien fue un gran admirador de David (1 R. 5.1), y le envió materiales y artesanos para que ayudaran en la construcción de su palacio en Jerusalén (2 S. 5.11; 1 Cr. 14.1)
Cuando Salomón ascendió al trono Hiram envió emisarios para hacer nuevos contactos, los que condujeron a un tratado comercial por medio del cual enviaba madera del Líbano y artesanos calificados para la construcción del nuevo templo en Jerusalén, a cambio de un pago anual, por parte de Salomón, de trigo y aceite (1 R. 5.2-11), que faltaban en las ciudades fenicias. Aparentemente requirió pagos adicionales de cebada y vino para el mantenimiento de los obreros tirios, que incluían técnicos familiarizados con el diseño y el teñido de telas, y que fueron enviados para instruir a los israelitas (2 Cr. 2.3-7).
[…]
Tratados semejantes, para reajustar las fronteras entre los estados, se conocen por acuerdos sirios primitivos (p. ej. Alalak).
[…]
Flavio Josefo
Aparte del AT hay una crónica del gobierno de Hiram escrita por Flavio Josefo (Ant. 8. 50-54; Contra Apionem 1. 17s) basada en los historiadores Menandro y Dío. Según esta fuente, Hiram (lxx Jiram, gr. Heiramos, Heirómos) era hijo de Abi baal, y reinó 34 años hasta su muerte a la edad de 53. La construcción del templo de Jerusalén comenzó en el 11º año de su reinado, e. d. el cuarto de Salomón (1 R. 6.1).
[…]
Josefo, al igual que Eupólemo y Alejandro Polihistor, habla de las cartas, que según se dice fueron guardadas en los archivos estatales de Tiro, que se escribieron Hiram y Salomón con motivo de la construcción del templo. También afirma Josefo que los dos reyes intercambiaron acertijos, hasta que Salomón fue derrotado por un joven tirio llamado Abdemón. Clemente de Alejandría y Taciano dicen que una hija de Hiram se casó con Salomón; cf. la declaración de que entre sus esposas se encontraban algunas sidonias (IR.11:1-2).»[12]
Ver HIRAM, EL ARQUITECTO DEL PRIMER TEMPLO
En el portal Se nos va de las manos…,realiza una crítica sobre los que utilizan la Biblia con fines cabalísticos, para proponer fechas del advenimiento de Cristo, o para mostrar que hay números escondidos en la Biblia.
«Los fundamentalistas generalmente se basan en la supuesta inspiración de los textos bíblicos para tratar de “profetizar” eventos futuros. Todo esto se hace bajo la segura guía de las cifras “inspiradas” que aparecen en la Biblia. El ejemplo más diáfano de esto es la forma como las diversas sectas de corte pentecostal y adventista se jactan de contar años y generaciones bíblicas para tratar de anticiparse al fin de este “sistema de cosas” o incluso, los evangélicos preparándose al “arrebatamiento” que supuestamente experimentarán los hijos de Dios en el fin del mundo.
No hay tiempo más desperdiciado que el que se gasta en estos cálculos, pues como mostraré con diversos ejemplos, nos daremos cuenta de que los “números” que aparecen en la Biblia no suelen ser más que cifras ridículas, inventadas torpemente por los redactores ya fueran judíos o cristianos.
[...]
¿Qué consecuencia trae la aparición de este error en la Biblia, para los ingenuos fundamentalistas que tratan de averiguar en las supuestas profecías la fecha del fin del mundo ?
Es simple. Los fundamentalistas están tratando con cifras del orden de 5000 años para sus torpes cálculos apocalípticos. Un error de un 6% en estos cálculos arroja una incertidumbre de cerca de 300 años.
Es decir, si un “estudioso” bíblico dice que la profecía bíblica arroja una fecha para la venida de Jesucristo de 1914, en realidad debería agregar la incertidumbre asociada; si llamamos Ta al tiempo del arrebatamiento o Tc al tiempo de inicio del reinado de Cristo, un fundamentalista debería decir algo como :
Ta = 1999 ± 600 años
Y un testigo de Jehová debería decir
Tc = 1914 ± 600 años.
¿Cómo sería la urgencia en la predicación si los testigos de Jehová fueran honestos y dijeran: “¡El tiempo está cerca… antes de 600 años empieza la batalla de Armagedón!”? ¿O si los evangélicos tuvieran que decir, “antes de 600 años seremos arrebatados por los cielos”?
Desde esta óptica es comprensible el por qué los cristianos llevan esperando en vano desde hace 2000 años, cual mansos borregos, la “Inminente (¡!) Segunda venida” de “Nuestro Señor” Jesucristo. Es comprensible también, por qué el “Siervo fiel y Discreto” (Los Estafadores Testigos de Jehová de Brooklin) hayan recibido la luz de la llegada del fin, en cerca de 5 ocasiones, y siempre hayan sido fechas erróneas. Los cristianos seguirán esperando el fin del mundo tal como lo llevan haciendo durante 2000 años por una razón muy simple… El fin nunca llegará.”»[13]
La replica a esta crítica es sencilla.El día y la hora de su retorno no lo conoce nadie. Jesús, en los tiempos de su humanidad también negó conocer ese momento. Es verdad que no debemos poner fecha y hora, y todos los que han puesto fecha han fallado.Pero el dijo que debíamos velar y orar para evitar caer en tentación antes de su venida. También esta el ejemplo (parábola) de las vírgenes insensatas, que no tuvieron sus lámparas llenas de aceite y cuando el novio vino se habían quedad dormidas y no pudieron celebrar la llegada del novio (Cristo)
Conclusión:
a. Respecto de Pi=3
Es probable que los hebreos no conocieran los decimales.Sin embargo hay algunos interrogantes que todavía no tengo respuesta:
a.1. Posibles respuestas
Un comentarista de un foro, comenta que:
«La Biblia se debe entender literalmente, pero debe ser leída con atención, y no hacerle decir lo que no dice….ni falla la inspiración divina. En este caso, hay que notar dos cosas por lo menos:
El cordón de 30 codos que ceñía la fuente alrededor, en ninguna parte dice que estaba justo en el borde superior.
La fuente tenía una forma semiesférica, y si este cordón estaba más abajo del borde, la circunferencia puede tener exactamente 30 codos, aunque el diámetro superior sea de 10 codos, al descender es menor.
a.2. En este caso, hay que notar dos cosas por lo menos:
1. El cordón de 30 codos que ceñía la fuente alrededor, en ninguna parte dice que estaba justo en el borde superior. La fuente tenía una forma semiesférica, y si este cordón estaba más abajo del borde, la circunferencia puede tener exactamente 30 codos, aunque el diámetro superior sea de 10 codos, al descender es menor.
2. Otra forma de aproximarse al problema es reconocer que pi es un número irracional, con infinitas cifras decimales no periódicas, lo cual hace que cualquier forma de escribirlo sea tan sólo una aproximación. Nunca se puede escribir de manera exacta, pero esto no quiere decir que sea erróneo, sino que depende del uso que se le dé al dato.
Se puede escribir 3,14; 3,1416; 3,14159265; etc. En este caso, decir que es sencillamente 3 es una buena aproximación para los fines descriptivos del texto, que se refiere a los muebles del Templo.»[14]
El valor de Pi cambia en las distintas culturas
«En el antiguo Egipto pi se consideraba como 3,1605, sin embargo en la antigua Babilonia era considerado como 3. Si hacemos un recorrido por la historia veremos que el número pi tenía un valor distinto para muchos de los pueblos y culturas» [15]

«Parece que fue W. Jones el primero que empleó la letra griega pi para designarlo en su libro “Introducción a las matemáticas” (1.706), por ser la inicial de la palabra periferia (circunferencia).
Los egipcios ya conocían que la relación entre el diámetro y la longitud de una circunferencia no se podía calcular con exactitud y la expresaron con 3 + 1/6 ó 3,16.
Muchos siglos después el gran Arquímedes de Siracusa diseñó el método de los polígonos inscritos y circunscritos para calcularlo, que comentaré más adelante.
Así obtuvo el valor de pi = 3 + 1 / 7 ó 22 / 7 = 3,1428
Ptolomeo calculó que pi = 3 + 1 / 8 + 1 / 60 = 3,14166
Los matemáticos árabes y chinos habían hallado que pi era igual a 3,1416
Este procedimiento estuvo vigente hasta el siglo XVII, a partir de aquí los matemáticos comenzaron a diseñar algoritmos de cálculo, en los que no interviene la circunferencia, cada vez más originales y eficientes y los progresos fueron relativamente rápidos, yo destacaría algunos como:
p = 2 x 2 x 4 x 4 x 6 x 6 x… Algoritmo de Wallis
2 3 x 3 x 5 x 5 x 7 x 7 x…
p = 1 + 1 + 1 +… Algoritmo de Leibniz
8 1 x 3 5 x 7 9 x 11
p2 = 1 + 1 + 1 + 1 +… + 1, o sea, p2 = 6 · S (1/n2) Algoritmo de Euler
6 4 9 25 n2

Así el número de decimales hallados de pi fue aumentando sin parar:
Van Ceule encontró 35 que hizo grabar en su tumba.
Sharp halló 72, Lagny: 127, Vega: 139, Rutherford llegó a los 208 en 1.841 y a 440 en 1.872, pero el británico William Shanks, que dedicó 20 años de su vida, estableció la última gran marca de los calculistas, digamos manuales, al llegar al decimal 707 en 1.874. Fue homenajeado como un héroe y se escribieron bajo la cúpula del palacio de la Découverte de Paris.
Desgraciadamente en el año 1.947, D. F. Ferguson descubrió que el decimal 528 era incorrecto, y obviamente todos los siguientes…
A partir de la década de los 40, la aparición de los ordenadores ha permitido profundizar, rápidamente, en el cálculo de pi, así en 1.949 se llegó a los 2.036 decimales, en 1.959 ya eran 10.000, en 1.974 se consiguieron obtener 1.000.000. Uno de los últimos récords sobrepasaba los 6 mil millones en 1.995.
Aquí tenéis, a título informativo, los 100 primeros decimales de pi que, obviamente, no aplicaréis en vuestros problemas geométricos, pero que siempre son curiosos de ver e, incluso, os pueden servir de entrenamiento memorístico. ¿Os atrevéis?
pi = 3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679…» [16]
«William James, Filósofo estadounidense, dijo dos cosas muy interesantes:
1 “Los decimales no calculados de pi, duermen en un misterioso reino abstracto, donde gozan de una débil realidad, hasta que no son calculados, no se convierten en algo plenamente real, e incluso entonces su realidad es mera cuestión de grado.”
2 “Si consideramos el mundo de relaciones geométricas, allí duerme el milésimo decimal de Pi, aunque jamás nadie trate de calcularlo.” » [17]
Me pregunto, que sentido tiene buscarle el milésimo decimal al número Pi, si no lo vas a usar. Así tiene que haber sido en el diseño y construcción del mar de bronce. Uso Pi=3 por dos razones posibles:
1. Tomó el modelo babilónico, que a lo mejor era el que el diseñador (Hiram) conocía.
2. o simplemente no necesitó los decimales por alguna razón que no se comprende bien.
Recordemos que Hiram era un hombre sabio, y conocía su oficio perfectamente bien.Y que como ya dijimos venia recomendado por el rey, como un hombre sabio que conocía muy bien su trabajo:
“Entonces Hiram rey de Tiro respondió por escrito que envió a Salomón: Porque Jehová amó a su pueblo, te ha puesto por rey sobre ellos. Además decía Hiram: Bendito sea Jehová el Dios de Israel, que hizo los cielos y la tierra, y que dio al rey David un hijo sabio, entendido, cuerdo y prudente, que edifique casa a Jehová, y casa para su reino. Yo, pues, te he enviado un hombre hábil y entendido, Hiram-abi, hijo de una mujer de las hijas de Dan, mas su padre fue de Tiro; el cual sabe trabajar en oro, plata, bronce y hierro, en piedra y en madera, en púrpura y en azul, en lino y en carmesí; asimismo sabe esculpir toda clase de figuras, y sacar toda forma de diseño que se le pida, con tus hombres peritos, y con los de mi señor David tu padre.” (2 Crónicas 2:11-14)
Tremenda recomendación y mas viniendo del Rey de Tiro, que eran una potencia comercial en aquella época!
Pero esto también nos enseña que no podemos interpretar la Biblia con nuestra mente occidental, ya que fue escrita en otra época y en otra cultura. Si no hacemos caso a esta advertencia, erraremos, y después nos acusarán de querer hacerle decir a la Biblia lo que la biblia no dice o no fue la intención del autor decir.
Lamentablemente, todos los hiper racionalistas criticones que tratan de negar la inerrancia de la Biblia, ni siquiera se acercan a ella con intenciones de hallar la verdad, sino mas bien con el único motivo de probar que es inexacta, errante, indigna de confianza, llena de errores, y mas aún.
«La novela Contacto de Carl Sagan —sobre la que luego se filmó la película homónima— toma a π (aunque no en base decimal) como un número que esconde la esencia misma del universo.»[18] Quizás tomar a Pi=3, sin decimales, puede significar un simbolismo de la trinidad, no digo que sea, pero es posible, ya que como expliqué antes este mar de bronce tenía un simbolismo, al ser consagrado a Dios: “Este enorme mar parece simbolizar el gran mar cósmico, que era para los antiguos la fuente de la vida y la fecundidad”»[19]
Ver ¿Es válida la teomática (el uso de los números para verificar la Biblia) como defensa de las Escrituras?
Lamentablemente, uno no tiene respuestas para los porqués de los seres humanos ni respuesta para todos los problemas matemáticos que surgen.

Paul Halmos
Para los porques de los seres humanos, solo tengo por respuesta sincera y verdadera que el único que conoce los corazones y escudriña las mentes es Dios y para los problemas matemáticos la respuesta que mas me gusta es la de una cita de Paul Halmos, matemático estadounidense nacido en Hungría en 1916, quien dijo una vez que “El corazón de las matemáticas son sus propios problemas“.[20]
Lo que me queda bien claro de esta investigación, es que la biblia de ningún modo ni en este pasaje ni en otro, está haciendo hincapié en un modelo matemático en desmedro de otro, y mucho menos en este relato, que lo mas importante es la construcción del templo del rey Salomón, por parte de un especialista altamente capacitado, recomendado por el rey de Tiro especialmente para el rey Salomón.Esa es la trama del contexto de este relato. De ahí en mas, solo leyendas de origen masónico que hablan de Hiram y sus posibles amores con la Reina de Saba, que culminaron en su supuesta muerte (ver Hiram Abiff)
También hay otras leyendas sobre El asesinato de Hiram Abif (ver HIRAM ABiF Leyenda o Realidad?), pero como explico, son TODAS LEYENDAS.
Hay que tener en cuenta que en el papiro egipcio Rhind, datado alrededor de 1650 a.C., ya se daba el valor de 3,16 para el número pi.[21]
Donald Page, físico católico de la Universidad de Alberta en Canadá, autor de trabajos conocidos en coautoría con el mítico Stephen Hawking.
Sobre los ataques a la Biblia por pi=3, Page puntualiza que el cociente entre el perímetro y el diámetro de un círculo es 3.1415… sólo cuando el círculo está dibujado en un plano. Pero en una superficie curva (o en un espacio curvo) la cosa no es así: para ir de un punto de un círculo trazado en la Tierra (un paralelo digamos) a su centro (el polo norte) el camino más directo (el radio) es por un meridiano, y se recorre una distancia mayor al radio del mismo círculo en un plano. ¿Se refiere la Biblia a un mar en un espacio curvo? Dudoso, pero “matemáticamente” posible.[22]
Pero yo averigue sobre esto si era posible y me respondió un científico español, el dr. M.Hernandez, especialista en zoología , que “el único problema es que para que el radio del “circulo curvo” se desviara significativamente de 3,1415… (aunque solo fuera unas décimas), debería ser varios órdenes de magnitud mayor que 30 codos de perímetro. En un círculo de ese tamaño, la curvatura del planeta es despreciable y ni loco llega a 3,0.”[23]
También un cristiano comentó en un debaate que surgió en un blog que “Sobre pi y otros asuntos: La Biblia es un libro de cronología e instrucciones, no un tratado de ingeniería. El que escribió fue un simple cronista, porque lo importante fue el relato de lo que se hizo, no cómo se hizo.” [24]
Una última cosa que debemos también comprender que se deduce de la lectura de la Biblia, y es que Israel estaba rodeado de países que estaban mas desarrollados en sus conocimientos científicos que Israel, Egipto y Babilonia tenían mas desarrollo del conocimiento que Israel. Israel solo superaba al resto de las naciones en su moral.
Esto ya se vislumbra desde los tiempos de Abraham. Pablo Hoff comenta al respecto “ Tanto el mundo antediluviano como el de la Torre de Babel ponen en relieve que no obstante el progreso material y el nacimiento de las civilizaciones, el hombre fracasaba moral y espiritualmente.”[25]
Artículos relacionados
Recomiendo http://tematicacristiana.blogspot.com/2010/04/dice-la-biblia-que-pi-3.html ,ya que esta actualizado
http://lasteologias.wordpress.com/2010/03/08/el-valor-de-pi-revelado-en-la-biblia/
Notas:
[0] Pablo Hoff, Los libros Históricos, Pág. 161, edit. vida, undécima impresión, 1993,EE.UU.
[1] Nuevo Diccionario Bíblico 1a. edición (basada en la segunda edición inglesa del New Bible Dictionary, 1982) , pág. 1333,Edit. Certeza
[2] http://es.wikipedia.org/wiki/N%C3%BAmero_real
[3] http://es.wikipedia.org/wiki/N%C3%BAmero_%CF%80
[4] <!--[endif]--> http://www.antesdelfin.com/foro/showthread.php?t=11099
[5] http://mensajeros.blog.com/2918097/
[6] Los libros Históricos, op. cit. pag. 161
[7] Nota al pie de página:1 Reyes 7:26 RV 1995
Nota:
También podes bajar una biblia electrónica gratis de internet y encontrar el artículo en esa biblia electrónica, en la traducción 1995 de reina Valera ( e-Sword® Version 7.8.5 Copyright © 2000-2007 Rick Meyers , 5902 Parham Road Franklin, TN 37064 United States of America www .e -sword .net )
[8] http://foros.monografias.com/showthread.php?t=33021&page=2&pp=10
[9] http://www.sindioses.org/humor/criticas.html
[10] http://www.dormilones.net/2007/06/13/pi-3-lo-pone-en-la-biblia/
[11] Nelson, Wilton M., (Hiram).Nuevo Diccionario Ilustrado de la Biblia, (Nashville, TN: Editorial Caribe) 2000, c1998.
[12] <!--[if gte mso 9]> Normal 0 21 false false false MicrosoftInternetExplorer4 <![endif]--><!--[if gte mso 9]> <![endif]--> <!--[endif]-->Nelson, Wilton M., (Hiram).Nuevo Diccionario Ilustrado de la Biblia, (Nashville, TN: Editorial Caribe) 2000, c1998.
[13] http://senosva.blogia.com/2007/102901-y-jesus-llegara….php
[14] http://it.answers.yahoo.com/question/index?qid=20080425060745AAElDZP (comentario de chess fan)
[15] http://humor.orange.es/delocos/curiosidades/ver_curiosidad.php?curiosidad=923
[16] http://www.xtec.es/~bfiguera/curioso6.html
[17] http://tematicacristiana.blogspot.com/2008/06/paul-halmos.html
[18] http://es.wikiquote.org/wiki/Matem%C3%A1tica
[19] Nota al pie de página:1 Reyes 7:26 RV 1995
[20] http://tematicacristiana.blogspot.com/2008/06/paul-halmos.html
[21] http://jolimu.wordpress.com/2008/03/24/eslabones-perdidos-juegan-al-escondido/#comment-598
[22] Física en la Biblia, Alberto Rojo – Diario Critica,http://www.nforo.net/showthread.php?p=441641
[23] http://oldearth.wordpress.com/2008/07/12/%C2%BFquien-insulta-a-quien/#comment-1826
[24] http://oldearth.wordpress.com/2008/07/12/%C2%BFquien-insulta-a-quien/#comment-1831
[25] Pablo Hoff, Pentateuco, pp.49,edit. Vida
 Re: ¿DICE LA BIBLIA QUE Pi = 3?
Re: ¿DICE LA BIBLIA QUE Pi = 3?
Cabalista, no es menos cierto que existen muchas teorias al respecto, pero la realidad matematica siempre nos va a llevar al GADU:.
En sintesis, todo lo creado se debe a una perfeccion que su exactitud aun hoy nos llega a asombrar, y precisamente debido a ello nosotros como seres humanos a veces no nos podemos poner en un plano de total entendimiento de la Divinidad; aun asi el Altisimo nos ha proporcionado con metodos como las matematicas y las ciencias para de una forma particular poder darnos un asomo de su grandeza y Omnisciencia.
Aprovecho la ocasion para darle una fraternal bienvenida a nuestro Taller Virtual.
En sintesis, todo lo creado se debe a una perfeccion que su exactitud aun hoy nos llega a asombrar, y precisamente debido a ello nosotros como seres humanos a veces no nos podemos poner en un plano de total entendimiento de la Divinidad; aun asi el Altisimo nos ha proporcionado con metodos como las matematicas y las ciencias para de una forma particular poder darnos un asomo de su grandeza y Omnisciencia.
Aprovecho la ocasion para darle una fraternal bienvenida a nuestro Taller Virtual.
 Re: ¿DICE LA BIBLIA QUE Pi = 3?
Re: ¿DICE LA BIBLIA QUE Pi = 3?
Como usted menciona, las dos columnas representan la entrada a una nueva vida que siempre se va a encaminar en pos de la Luz, de la Verdadera Luz; y nosotros como iniciados en estos sagrados misterios tenemos la oportunidad de poder engrandecer con nuestra labor a todos los HH:. que nos acompanan por este sendero y principalmente al resto de la Humanidad.
Seria una verdadera satisfaccion que muchas personas pudieran adentrarse en este camino de la Verdad y la Luz. Por lo menos nosotros como maestros masones, tenemos esa posibilidad y nunca debemos dejar a un lado las sublimes ensenanzas de nuestra augusta Orden.
Seria una verdadera satisfaccion que muchas personas pudieran adentrarse en este camino de la Verdad y la Luz. Por lo menos nosotros como maestros masones, tenemos esa posibilidad y nunca debemos dejar a un lado las sublimes ensenanzas de nuestra augusta Orden.
 Re: ¿DICE LA BIBLIA QUE Pi = 3?
Re: ¿DICE LA BIBLIA QUE Pi = 3?
mis saludos a todas las personas que leen estas cosas, es muy grato para mi contribuir en este sitio. Como se mencioa en la cabala "todo es numeros, todo es matemáticas". La pregunta en cuanto a los 2 testigos...que pasaria si las personas ven en Jerusalen a estos 2 testigos y a un nuevo templo construido según el modelo de Salomón? no dejaria de ser una teoria?
Página 1 de 1.
Permisos de este foro:
No puedes responder a temas en este foro.


» Cines de Cuba
» Visita del MRGM Ernesto Zamora a la Logia Renacer No. 410
» Spectre (2015) - Original Soundtrack Extended
» LAS LOGIAS EN CUBA
» 200th Class Reunion November 3 & 4
» 200th Class Reunion Cap and Ring Ceremony
» Fraternidad UD Primera Sesión 21 de Noviembre de 2019
» Knights of St. Andrew Valle de Miami, Oriente de la Florida